题目内容
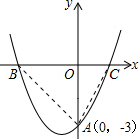
二次函数y=ax2+bx+c的图象与x轴交于B、C两点，与y轴交于A点．
（1）根据图象确定a、b、c的符号，并说明理由；
（2）如果点A的坐标为（0，-3），∠ABC=45°，∠ACB=60°，求这个二次函数的解析式．
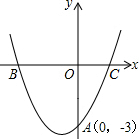
（1）根据图象确定a、b、c的符号，并说明理由；
（2）如果点A的坐标为（0，-3），∠ABC=45°，∠ACB=60°，求这个二次函数的解析式．
（1）∵抛物线开口向上
∴a＞0
又∵对称轴在y轴的左侧
∴
＜0，
∴b＞0
又∵抛物线交y轴的负半轴
∴c＜0
（2）连接AB，AC
∵在Rt△AOB中，∠ABO=45°
∴∠OAB=45°，
∴OB=OA
∴B（-3，0）
又∵在Rt△ACO中，∠ACO=60°
∴OC=OAcot=60°=
∴C（
，0）
设二次函数的解析式为y=ax2+bx+c（a≠0）
由题意：
?
∴所求二次函数的解析式为y=
x2+（
-1）x-3．
∴a＞0
又∵对称轴在y轴的左侧
∴
| b |
| -2a |
∴b＞0
又∵抛物线交y轴的负半轴
∴c＜0
（2）连接AB，AC
∵在Rt△AOB中，∠ABO=45°
∴∠OAB=45°，
∴OB=OA
∴B（-3，0）
又∵在Rt△ACO中，∠ACO=60°
∴OC=OAcot=60°=
| 3 |
∴C（
| 3 |
设二次函数的解析式为y=ax2+bx+c（a≠0）
由题意：
|
|
∴所求二次函数的解析式为y=
| ||
| 3 |
| 3 |
练习册系列答案
相关题目
点C，B的横坐标，且此抛物线过点A（3，6）．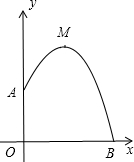
图）如果抛物线的最高点M离墙1米，离地面
