题目内容
如图,抛物线y=
x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,-4).
(1)求抛物线的解析式;
(2)点Q是线段OB上的动点,过点Q作QE∥BC,交AC于点E,连接CQ,设OQ=m,当△CQE的面积最大时,求m的值,并写出点Q的坐标;
(3)若平行于x轴的动直线,与该抛物线交于点P,与直线BC交于点F,D的坐标为(-2,0),则是否存在这样的直线l,使OD=DF?若存在,求出点P的坐标;若不存在,请说明理由.

| 1 |
| 2 |
(1)求抛物线的解析式;
(2)点Q是线段OB上的动点,过点Q作QE∥BC,交AC于点E,连接CQ,设OQ=m,当△CQE的面积最大时,求m的值,并写出点Q的坐标;
(3)若平行于x轴的动直线,与该抛物线交于点P,与直线BC交于点F,D的坐标为(-2,0),则是否存在这样的直线l,使OD=DF?若存在,求出点P的坐标;若不存在,请说明理由.

(1)把x=2,y=0;x=0,y=-4代入y=
x2+bx+c,
得
解得
故所求抛物线的解析式为y=
x2+x-4.
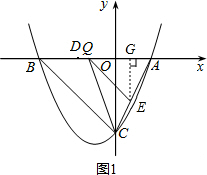
(2)如图1,作EG⊥AQ于点G,由(1)可知,点B的坐标为(-4,0).
∴CO=4,AB=6,AQ=m+2.
∵QE∥BC,
∴△AEQ∽△ACB.
∴
=
,即
=
.
∴EG=
.
∴S△CQE=S△ACQ-S△AEQ=
AQ•CO-
AQ•EG=
(m+2)(4-
),
=-
m2+
m+
=-
(m-1)2+3.
当m=1时,当△CQE的面积最大.
此时,点Q的坐标为(-1,0).
(3)若存在,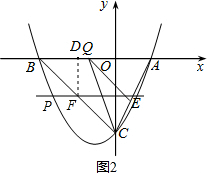 如图2,
如图2,
∵点B的坐标为(-4,0),D的坐标为(-2,0),DO=DF,
∴DB=DF.∴∠ABC=∠BFD.
∵OC=OB,∠ABC=∠BCO=45°.
∴∠ABC=∠BFD=45°.
∴FD⊥AB.
则F(-2,-2).
∴
x2+x-4=-2.
解得x1=-1-
,x2=-1+
.
所以点P的坐标为(-1-
,-2)或(-1+
,-2).
| 1 |
| 2 |
得
|
解得
|
故所求抛物线的解析式为y=
| 1 |
| 2 |
(2)如图1,作EG⊥AQ于点G,由(1)可知,点B的坐标为(-4,0).
∴CO=4,AB=6,AQ=m+2.
∵QE∥BC,
∴△AEQ∽△ACB.
∴
| EG |
| CO |
| AQ |
| AB |
| EG |
| 4 |
| m+2 |
| 6 |
∴EG=
| 2m+4 |
| 3 |
∴S△CQE=S△ACQ-S△AEQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2m+4 |
| 3 |
=-
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
当m=1时,当△CQE的面积最大.
此时,点Q的坐标为(-1,0).
(3)若存在,
 如图2,
如图2,∵点B的坐标为(-4,0),D的坐标为(-2,0),DO=DF,
∴DB=DF.∴∠ABC=∠BFD.
∵OC=OB,∠ABC=∠BCO=45°.
∴∠ABC=∠BFD=45°.
∴FD⊥AB.
则F(-2,-2).
∴
| 1 |
| 2 |
解得x1=-1-
| 5 |
| 5 |
所以点P的坐标为(-1-
| 5 |
| 5 |


练习册系列答案
相关题目



 费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?
费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?