题目内容
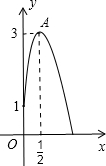
如图所示是二次函数y=-x2+4x图象上的一段，其中0≤x≤4、若矩形ABCD的两个顶点A，B落在x轴上，另外两个顶点C，D落在函数图象上，则矩形ABCD的周长能否恰好为8？若能，请求出C，D两点坐标；若不能，请说明理由．
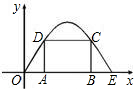
假设周长恰好是8，设点A的横坐标为x，
∵y=-x2+4x，
∴顶点横坐标为-
=2，
∴点B的横坐标为2+（2-x）=4-x，
∴AB=4-x-x=4-2x；
∴D点纵坐标为-x2+4x，
即AD=-x2+4x；
∴AD+AB=-x2+4x+（4-2x）=
×8，
∴x=0或2；
∴当x=0时，-x2+4x=0，D和C点纵坐标为0，构不成矩形．
∴当x=2时，-x2+4x=4，只有一个最高点存在，同样构不成矩形，
综合可知，与能构成矩形矛盾，故不存在．
∵y=-x2+4x，
∴顶点横坐标为-
| 4 |
| 2×(-1) |
∴点B的横坐标为2+（2-x）=4-x，
∴AB=4-x-x=4-2x；
∴D点纵坐标为-x2+4x，
即AD=-x2+4x；
∴AD+AB=-x2+4x+（4-2x）=
| 1 |
| 2 |
∴x=0或2；
∴当x=0时，-x2+4x=0，D和C点纵坐标为0，构不成矩形．
∴当x=2时，-x2+4x=4，只有一个最高点存在，同样构不成矩形，
综合可知，与能构成矩形矛盾，故不存在．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
