题目内容
如图,二次函数y=
x2+bx-
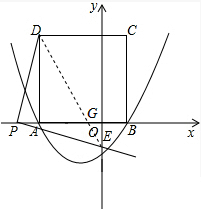
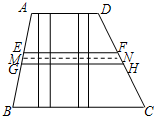
的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标:______;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.

| 1 |
| 2 |
| 3 |
| 2 |
(1)请直接写出点D的坐标:______;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.

(1)(-3,4);
(2)设PA=t,OE=l
由∠DAP=∠POE=∠DPE=90°得△DAP∽△POE
∴
=
 ∴l=-
∴l=-
t2+
t=-
(t-
)2+
∴当t=
时,l有最大值
即P为AO中点时,OE的最大值为
;
(3)存在.
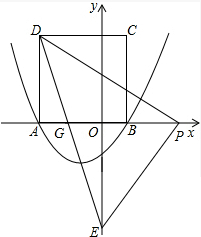
①点P点在y轴左侧时,DE交AB于点G,
P点的坐标为(-4,0),
∴PA=OP-AO=4-3=1,
 由△PAD≌△EOP得OE=PA=1
由△PAD≌△EOP得OE=PA=1
∵△ADG∽△OEG
∴AG:GO=AD:OE=4:1
∴AG=
AO=
∴重叠部分的面积=
×4×
=
②当P点在y轴右侧时,P点的坐标为(4,0),
此时重叠部分的面积为
(2)设PA=t,OE=l
由∠DAP=∠POE=∠DPE=90°得△DAP∽△POE
∴
| 4 |
| 3-t |
| t |
| l |
 ∴l=-
∴l=-| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 9 |
| 16 |
∴当t=
| 3 |
| 2 |
| 9 |
| 16 |
即P为AO中点时,OE的最大值为
| 9 |
| 16 |
(3)存在.
①点P点在y轴左侧时,DE交AB于点G,
P点的坐标为(-4,0),
∴PA=OP-AO=4-3=1,
 由△PAD≌△EOP得OE=PA=1
由△PAD≌△EOP得OE=PA=1∵△ADG∽△OEG
∴AG:GO=AD:OE=4:1
∴AG=
| 4 |
| 5 |
| 12 |
| 5 |
∴重叠部分的面积=
| 1 |
| 2 |
| 12 |
| 5 |
| 24 |
| 5 |
②当P点在y轴右侧时,P点的坐标为(4,0),
此时重叠部分的面积为
| 712 |
| 77 |

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目


 费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?
费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?