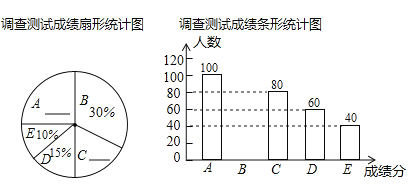
题目内容
【题目】如图,有一菱形纸片ABCD,∠A=60°,将该菱形纸片折叠,使点A恰好与CD的中点E重合,折痕为FG,点F、G分别在边AB、AD上,联结EF,那么cos∠EFB的值为____.
【答案】![]()
【解析】
连接BE,由菱形和折叠的性质,得到AF=EF,∠C=∠A=60°,由cos∠C=![]() ,
,![]() ,得到△BCE是直角三角形,则
,得到△BCE是直角三角形,则![]() ,则△BEF也是直角三角形,设菱形的边长为
,则△BEF也是直角三角形,设菱形的边长为![]() ,则EF=
,则EF=![]() ,
,![]() ,由勾股定理,求出FB=
,由勾股定理,求出FB=![]() ,则
,则![]() ,即可得到cos∠EFB的值.
,即可得到cos∠EFB的值.
解:如图,连接BE,

∵四边形ABCD是菱形,
∴AB=BC=CD,∠C=∠A=60°,AB∥DC,
由折叠的性质,得AF=EF,
则EF=AB![]() FB,
FB,
∵cos∠C=![]() ,
,
∵点E是CD的中线,
∴![]() ,
,
∴![]() ,
,
∴△BCE是直角三角形,即BE⊥CD,
∴BE⊥AB,即△BEF是直角三角形.
设BC=m,则BE=![]() ,
,
在Rt△BEF中,EF=![]() ,
,
由勾股定理,得:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
则![]() ,
,
∴ ;
;
故答案为:![]() .
.

练习册系列答案
相关题目