题目内容
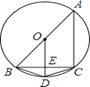
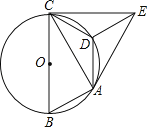
【题目】如图,已知⊙O是△ABC的外接圆,且BC为⊙O的直径,在劣弧![]() 上取一点D,使
上取一点D,使![]() ,将△ADC沿AD对折,得到△ADE,连接CE.
,将△ADC沿AD对折,得到△ADE,连接CE.
(1)求证:CE是⊙O的切线;
(2)若CE![]() C D,劣弧
C D,劣弧![]() 的弧长为π,求⊙O的半径.
的弧长为π,求⊙O的半径.
【答案】(1)见解析;(2)圆的半径为3.
【解析】
(1)在△ACE中,根据三角形内角和为180°,则2α+2β+2γ=180°,即可求解;
(2)证明四边形AMCN为矩形,![]() ,而AB=x,则
,而AB=x,则
sin∠ABM=![]() ,即∠ABM=60°,即可求解.
,即∠ABM=60°,即可求解.
(1)∵![]() ,∴∠CAD=∠BCA=α=∠EAD,
,∴∠CAD=∠BCA=α=∠EAD,
设:∠DCA=∠DEA=β,∠DCE=∠DEC=γ,
则△ACE中,根据三角形内角和为180°,
∴2α+2β+2γ=180°,
∴α+β+γ=90°,
∴CE是⊙O的切线;
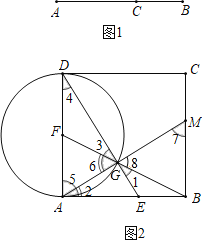
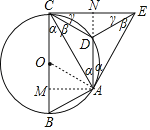
(2)过点A作AM⊥BC,延长AD交CE于点N,
则DN⊥CE,∴四边形AMCN为矩形,
设:AB=CD=x,则CE![]() x,
x,
则CN![]() CE
CE![]() x=AM,而AB=x,
x=AM,而AB=x,
则sin∠ABM![]() ,∴∠ABM=60°,
,∴∠ABM=60°,
∴△OAB为等边三角形,即∠AOB=60°,
![]() 2πr=π,
2πr=π,
解得:r=3,
故圆的半径为3.

练习册系列答案
相关题目
【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 | m | 40% |
合格 | 6 | n% |
待合格 | 3 | 6% |
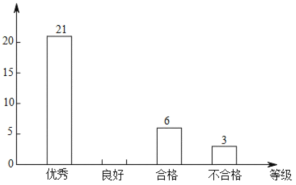
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了 名学生;表中m= ,n= ;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.