题目内容
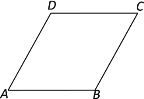
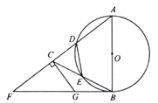
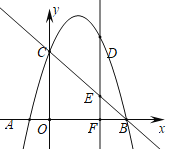
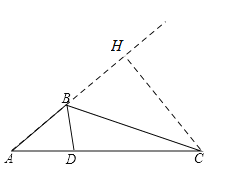
【题目】如图,![]() 的角平分线
的角平分线![]() ,
,![]() ,
,![]() 、
、![]() 所对的边记为
所对的边记为![]() 、
、![]() .
.
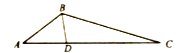
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() 的面积(用含
的面积(用含![]() ,
,![]() 的式子表示即可);
的式子表示即可);
(3)求证:![]() ,
,![]() 之和等于
之和等于![]() ,
,![]() 之积.
之积.
【答案】(1)2;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,利用直角三角形30度角的性质可知BE长,得
,利用直角三角形30度角的性质可知BE长,得![]() ,即点E、点D重合,中线与高线重合,可知AB=AC,即
,即点E、点D重合,中线与高线重合,可知AB=AC,即![]() ;
;
(2)表示方法有两种,可能情形1:过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 延长线于点
延长线于点![]() ,解直角三角形可得
,解直角三角形可得![]() ,
,![]() ,利用三角形面积公式可得
,利用三角形面积公式可得
![]() 和
和![]() 的面积相加即可;可能情形2:过点
的面积相加即可;可能情形2:过点![]() 作
作![]() 于点
于点![]() ,解直角三角形可得
,解直角三角形可得![]() ,直接利用三角形面积公式求解即可;
,直接利用三角形面积公式求解即可;
(3)由(2)中面积的两种表示方法可直接证得结论.
解:(1)过点![]() 作
作![]() 于点
于点![]()
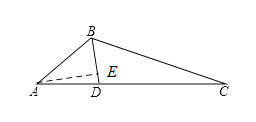
∵![]() 平分
平分![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∵![]() ,∴点
,∴点![]() 与点
与点![]() 重合,∴
重合,∴![]() .
.
∴![]() .
.
(2)答案不唯一.
可能情形1:过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 延长线于点
延长线于点![]()
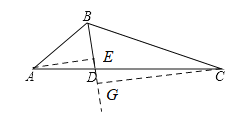
∵![]() 平分
平分![]() ,∴
,∴![]() .
.
∵在![]() 中,
中,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]()
∴![]()
![]() .
.
可能情形2:过点![]() 作
作![]() 于点
于点![]() ,用含
,用含![]() 的式子表示出
的式子表示出![]() ,
,
于是![]() .
.
(3)从上面![]() 两种面积表示方法
两种面积表示方法![]() ,
,![]() ,可得
,可得![]() ,化简得
,化简得![]() ,即
,即![]() ,
,![]() 之和等于
之和等于![]() ,
,![]() 之积.
之积.

 阅读快车系列答案
阅读快车系列答案【题目】某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资![]() (结果保留整数),并判断
(结果保留整数),并判断![]() 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.