题目内容
【题目】综合与实践—探究正方形旋转中的数学问题
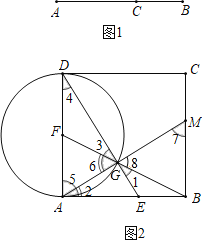
问题情境:已知正方形![]() 中,点
中,点![]() 在
在![]() 边上,且
边上,且![]() .将正方形
.将正方形![]() 绕点
绕点![]() 顺时针旋转得到正方形
顺时针旋转得到正方形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 分别是点
分别是点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
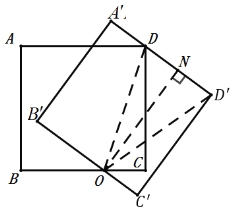
特例分析:(1)“乐思”小组提出问题:如图1,当点![]() 落在正方形
落在正方形![]() 的对角线
的对角线![]() 上时,设线段
上时,设线段![]() 与
与![]() 交于点
交于点![]() .求证:四边形
.求证:四边形![]() 是矩形;
是矩形;
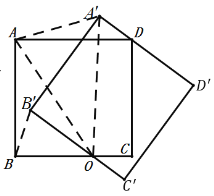
(2)“善学”小组提出问题:如图2,当线段![]() 经过点
经过点![]() 时,猜想线段
时,猜想线段![]() 与
与![]() 满足的数量关系,并说明理由;
满足的数量关系,并说明理由;
深入探究:(3)请从下面![]() ,
,![]() 两题中任选一题作答.我选择题.
两题中任选一题作答.我选择题.
A.在图2中连接![]() 和
和![]() ,请直接写出
,请直接写出![]() 的值.
的值.
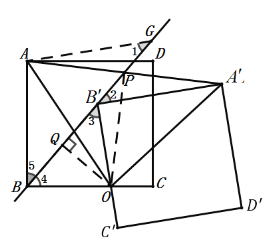
B.“好问”小组提出问题:如图3,在正方形![]() 绕点
绕点![]() 顺时针旋转的过程中,设直线
顺时针旋转的过程中,设直线![]() 交线段
交线段![]() 于点
于点![]() .连接
.连接![]() ,并过点
,并过点![]() 作
作![]() 于点
于点![]() .请在图3中补全图形,并直接写出
.请在图3中补全图形,并直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)A.
;(3)A.![]() ,B.
,B.![]() .
.
【解析】
(1)根据旋转性质证得![]() ,从而证得绪论;
,从而证得绪论;
(2)连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,根据旋转性质结合三角形三线合一的性质证得
,根据旋转性质结合三角形三线合一的性质证得![]() ,再证得四边形
,再证得四边形![]() 是矩形,从而求得结论;
是矩形,从而求得结论;
(3)A. 设![]() ,根据旋转性质结合两边对应成比例且夹角相等证得
,根据旋转性质结合两边对应成比例且夹角相等证得![]() ,利用相似三角形对应边成比例再结合勾股定理即可求得答案;
,利用相似三角形对应边成比例再结合勾股定理即可求得答案;
B. 作![]() 交直线
交直线![]() 于点
于点![]() ,根据旋转性质利用AAS证得
,根据旋转性质利用AAS证得![]() ,证得OP是线段
,证得OP是线段![]() 的中垂线,根据旋转性质结合两边对应成比例且夹角相等证得
的中垂线,根据旋转性质结合两边对应成比例且夹角相等证得![]() ,利用相似三角形对应高的比等于相似比再结合勾股定理即可求得答案;
,利用相似三角形对应高的比等于相似比再结合勾股定理即可求得答案;
(1)由题意得:![]() ,
,![]() ,
,
由旋转性质得:![]() ,
,
∵![]()
![]()
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
(2)连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于N,
于N,
由旋转得:![]() ,
,
∵![]() ,
,
![]() ,
,
∵ON⊥D![]() ,∠
,∠![]() =∠
=∠![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ;
;
(3)A.如图,连接![]() ,
,![]() ,
,![]() ,
,
由旋转的性质得:∠BO![]() =∠
=∠![]() ,BO= O
,BO= O![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
![]()
![]()
B.如图,过点![]() 作AG∥
作AG∥![]() 交直线
交直线![]() 于点G,过点O作
于点G,过点O作![]() 交直线
交直线![]() 于点
于点![]() ,连接OP,
,连接OP,
∵AG∥![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形 ,
是正方形 ,
由旋转可知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,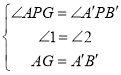
![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又∵![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 设
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,由勾股定理可得:
中,由勾股定理可得:
![]() ,
,
![]() .
.

 名师金手指领衔课时系列答案
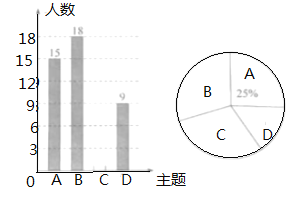
名师金手指领衔课时系列答案【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示,请根据图表信息解答下列问题:
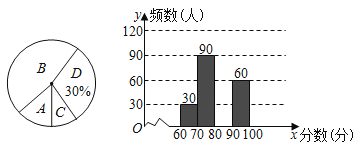
组别 | 分数段(分) | 频数 |
A组 | 60≤x<70 | 30 |
B组 | 70≤x<80 | 90 |
C组 | 80≤x<90 | m |
D组 | 90≤x<100 | 60 |
(1)本次调查的总人数为 人.
(2)补全频数分布直方图;
(3)若A组学生的平均分是65分,B组学生的平均分是75分,C组学生的平均分是85分,D出学生的平均分是95分,请你估计参加本次测试的同学们平均成绩是多少分?
【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 480 | 600 | 1800 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.6 | 0.6 | 0.6 |
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为 ;
(3)试估算盒子里黑、白两种颜色的球各有多少个?