题目内容
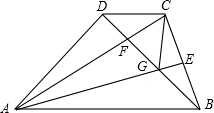 如图,在梯形ABCD中,DC∥AB,AB=AC,E为BC的中点,BD交AC于F,交AE于G,连接CG.下列结论中:
如图,在梯形ABCD中,DC∥AB,AB=AC,E为BC的中点,BD交AC于F,交AE于G,连接CG.下列结论中:
①AE平分∠BAC,②BG=CG,③CD=CG,④若BG=6,FG=4,则DF=5,⑤DC:AB=1:3,正确的有
- A.2个
- B.3个
- C.4个
- D.5个
B
分析:根据已知条件和“等腰三角形三线合一”,逐个进行验证,即可得出结论.
解答:∵梯形ABCD中,DC∥AB,AB=AC,E为BC的中点,
∴①AE平分∠BAC,正确;
∵AB=AC,E为BC的中点,
∴AE⊥BC,AE是BC的垂直平分线,
∴②BG=CG,正确;
延长CG与AB相交于H,
∵CG=GB,
∴∠HCB=∠DBC,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠ACH=∠ABG,
∵BG=CG,∠FGC=∠BGH,
∴△CGF≌△BGH,
∴GH=FG=4,CG=6,
∵AB∥CD,
∴△DCG∽△BGH,
∴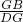 =
=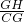 ,即
,即 =
= ,
,
解得DF=5,故④正确.
③⑤无法判断,
故选B
点评:此题很简单,考查的是等腰三角形的性质,即三线合一.
分析:根据已知条件和“等腰三角形三线合一”,逐个进行验证,即可得出结论.
解答:∵梯形ABCD中,DC∥AB,AB=AC,E为BC的中点,
∴①AE平分∠BAC,正确;
∵AB=AC,E为BC的中点,
∴AE⊥BC,AE是BC的垂直平分线,
∴②BG=CG,正确;
延长CG与AB相交于H,
∵CG=GB,
∴∠HCB=∠DBC,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠ACH=∠ABG,
∵BG=CG,∠FGC=∠BGH,
∴△CGF≌△BGH,
∴GH=FG=4,CG=6,

∵AB∥CD,
∴△DCG∽△BGH,
∴
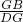 =
=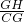 ,即
,即 =
= ,
,解得DF=5,故④正确.
③⑤无法判断,
故选B
点评:此题很简单,考查的是等腰三角形的性质,即三线合一.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=