题目内容
 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.求:梯形ABCD的周长.
分析:先作DH⊥BC于点H,得四边形ABHD是矩形,则BH=AD=2,CH=8,再由勾股定理求出DH,即求出AB,从而求出梯形ABCD的周长.
解答: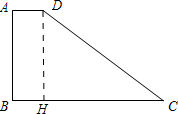 解:作DH⊥BC于点H,
解:作DH⊥BC于点H,
根据题意,得四边形ABHD是矩形,BH=AD=2,
∵BC=10,
∴CH=BC-BH=10-2=8,
∵CD=10,
∴DH=
=6,
∴AB=DH=6,
∴梯形ABCD的周长为:AD+AB+BC+CD=2+6+10+10=28.
答:梯形ABCD的周长为28.
 解:作DH⊥BC于点H,
解:作DH⊥BC于点H,根据题意,得四边形ABHD是矩形,BH=AD=2,
∵BC=10,
∴CH=BC-BH=10-2=8,
∵CD=10,
∴DH=
| CD2-CH2 |
∴AB=DH=6,
∴梯形ABCD的周长为:AD+AB+BC+CD=2+6+10+10=28.
答:梯形ABCD的周长为28.
点评:此题考查的知识点是直角梯形、勾股定理及矩形的判定与性质,关键是先作辅助线得矩形,再用勾股定理求AB.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
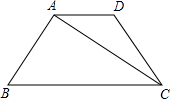 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.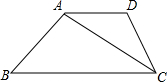 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,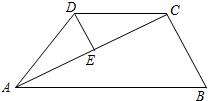 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=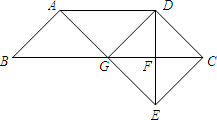 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.