Question

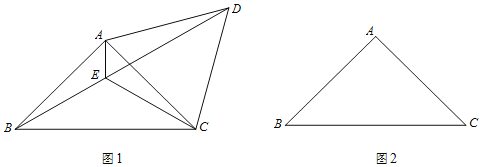
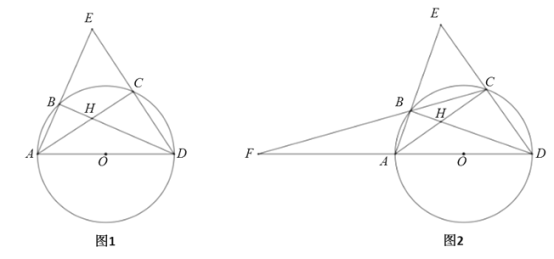
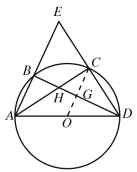
【题目】如图1，内接于,AD是直径，的平分线交BD于H，交于点C，连接DC并延长，交AB的延长线于点E.

（1）求证：；

（2）若，求的值

（3）如图2，连接CB并延长，交DA的延长线于点F，若，求的面积.

Answer 1

【答案】（1）见解析；（2） ；（3）

【解析】

（1）根据直径所对的圆周角是直角可得，然后利用ASA判定△ACD≌△ACE即可推出AE=AD；

（2）连接OC交BD于G，设，根据垂径定理的推论可得出OC垂直平分BD，进而推出OG为中位线，再判定，利用对应边成比例即可求出的值；

（3）连接OC交BD于G，由（2）可知：OC∥AB，OG=AB，然后利用ASA判定△BHA≌△GHC，设，则，再判定，利用对应边成比例求出m的值，进而得到AB和AD的长，再用勾股定理求出BD，可求出△BED的面积，由C为DE的中点可得△BEC为△BED面积的一半，即可得出答案.

（1）证明：∵AD是的直径

∵AC平分

在△ACD和△ACE中，

∵∠ACD=∠ACE，AC=AC，∠DAC=∠EAC

∴△ACD≌△ACE（ASA）

（2）如图，连接OC交BD于G，

，设，

则，OC=AD=

∴OC垂直平分BD

又∵O为AD的中点

∴OG为△ABD的中位线

∴OC∥AB，OG=，CG=

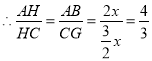
（3）如图，连接OC交BD于G，

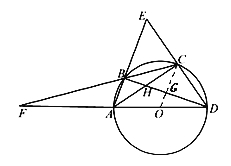
由（2）可知：OC∥AB，OG=AB

∴∠BHA=∠GCH

在△BHA和△GHC中，

∵∠BHA=∠GCH，AH=CH，∠BHA=∠GHC

∴

设，则

又，

∴

，

∵AD是的直径

又