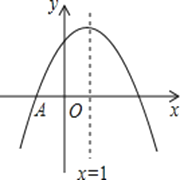题目内容
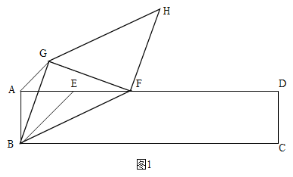
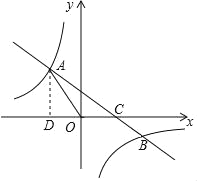
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)点E是x轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点的坐标.
【答案】(1)y=﹣![]() ,y=﹣
,y=﹣![]() x+2;(2)6;(3)当点E(﹣4,0)或(
x+2;(2)6;(3)当点E(﹣4,0)或(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣
,0)或(﹣![]() ,0)时,△AOE是等腰三角形.
,0)时,△AOE是等腰三角形.
【解析】
(1)利用待定系数法,即可得到反比例函数和一次函数的解析式;
(2)利用一次函数解析式求得C(4,0),即OC=4,即可得出△AOB的面积=![]() ×4×3=6;
×4×3=6;
(3)分类讨论:当AO为等腰三角形腰与底时,求出点E坐标即可.
(1)如图,在Rt△OAD中,∠ADO=90°,
∵tan∠AOD=![]() ,AD=3,
,AD=3,
∴OD=2,
∴A(﹣2,3),

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】下表中有两种移动电话计费方式.
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟![]() 是正整数
是正整数![]() .
.
![]() 当
当![]() 时,按方式一计费为______元;按方式二计费为______元;
时,按方式一计费为______元;按方式二计费为______元;
![]() 当
当![]() 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
![]() 当
当![]() 时,请直接写出省钱的计费方式?
时,请直接写出省钱的计费方式?
【题目】某甜品店用 A,B 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品 x 份,乙款甜品 y 份,共用去A 原料 2000 克.
原料 款式 | A 原料(克) | B 原料(克) |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
(1)求 y 关于 x 的函数表达式.
(2)已知每份甲甜品的利润为 a 元(a 正整数), 每份乙甜品的利润为 2 元. 假设两款甜品均能全部卖出.
①当 a=3 时,若获得总利润不少于 220 元,则至少要用去 B 原料多少克?
②现有 B 原料 3100 克,要使获利为 450 元且尽量不浪费原材料,甲甜品的每份利润应定为多元?