题目内容
【题目】如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需要绕行B地，已知B地位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向，若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长（结果保留整数）（参考数据：sin67°≈0.92；cos67°≈0.38；
≈1.73）
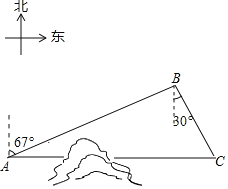
【答案】A地到C地之间高铁线路的长为592km．
【解析】
过点B作BD⊥AC于点D，利用锐角三角函数的定义求出AD及CD的长，进而可得出结论．
过点B作BD⊥AC于点D，
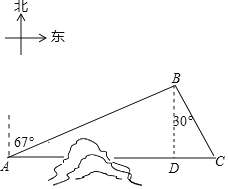
∵B地位于A地北偏东67°方向，距离A地520km，
∴∠ABD＝67°，
∴AD＝ABsin67°＝520×0.92＝478.4km，
BD＝ABcos67°＝520×0.38＝197.6km．
∵C地位于B地南偏东30°方向，
∴∠CBD＝30°，
∴CD＝BDtan30°＝197.6×
≈113.9km，
∴AC＝AD+CD＝478.4+113.9≈592（km）．
答：A地到C地之间高铁线路的长为592km．
练习册系列答案
相关题目
【题目】甲、乙两家商场平时以同样的价格出售相同的商品.“五一”节期间两家商场都让利酬宾.在甲商场按累计购物金额的
收费；在乙商场累计购物金额超过
元后，超出元的部分按
收费．设小红在同一商场累计购物金额为
元，其中
．
（1）根据题意，填写下表(单位：元)：
累计购物金额 |
|
|
| ··· |
在甲商场实际花费 |
| ··· | ||
在乙商场实际花费 |
| ··· |
（2）设小红在甲商场实际花费
元，在乙商场实际花费
元，分别求
关于的函数解析式；
（3）“五一”节期间小红如何选择这两家商场去购物更省钱？
