Question

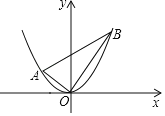
【题目】抛物线y＝﹣x2与直线y＝kx﹣2k+3交于A，B两点，若∠AOB＝90°，求k的值．

Answer 1

【答案】

【解析】

将y＝kx﹣2k+3代入y＝x2，得x2﹣kx+2k﹣3＝0，根据二次函数图象上点的坐标特征以及根与系数的关系得出y1＝x12，y2＝x22，x1x2＝4k﹣6，那么y1y2＝k2﹣3k+，当∠AOB＝90°时，过点A作AM⊥x轴于点M，过点B作BN⊥x轴于点N，证明△AOM∽△OBN，根据相似三角形对应边成比例得出y1y2＝﹣x1x2，依此列出关于k的方程，求出k的值即可．

解：将y＝kx﹣2k+3代入y＝x2，得x2﹣kx+2k﹣3＝0，

设抛物线y＝﹣x2与直线y＝kx﹣2k+3交于A（x1，y1），B（x2，y2）两点，

∴y1＝x12，y2＝x22，x1x2＝4k﹣6，

∴y1y2＝（x12）（x22）＝（x1x2）2＝（4k﹣6）2＝4k2﹣6k+9

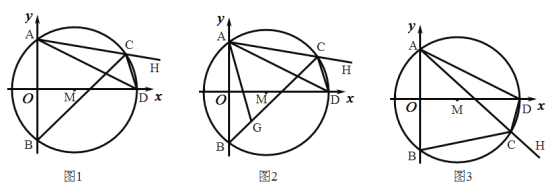
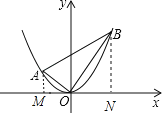
当∠AOB＝90°时，如图：

，

过点A作AM⊥x轴于点M，过点B作BN⊥x轴于点N．

在△AOM与△OBN中，

，

∴△AOM∽△OBN，

∴，即，

∴y1y2＝﹣x1x2，

∴4k2﹣6k+9＝﹣4k+6，

∵k＞0，

∴k＝，