题目内容
【题目】如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为________.
【答案】4![]()
【解析】
首先由对边分别平行可判断四边形ABCD为平行四边形,连接AC和BD,过A点分别作DC和BC的垂线,垂足分别为F和E,通过证明△ADF≌△ABC来证明四边形ABCD为菱形,从而得到AC与BD相互垂直平分,再利用勾股定理求得BD长度.
解:连接AC和BD,其交点为O,过A点分别作DC和BC的垂线,垂足分别为F和E,
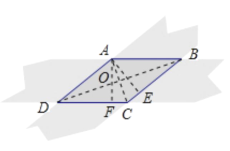
∵AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,
∴∠ADF=∠ABE,
∵两纸条宽度相同,
∴AF=AE,
∵
∴△ADF≌△ABE,
∴AD=AB,
∴四边形ABCD为菱形,
∴AC与BD相互垂直平分,
∴BD=![]()
故本题答案为:4![]()

练习册系列答案
相关题目