题目内容
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2
(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求y=-2x2+5x-3函数的“旋转函数”.
小明是这样思考的:由y=-2x2+5x-3函数可知,a1=-2,b1=5,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面的问题:
(1)写出函数y=-2x2+5x-3的“旋转函数”;
(2)若函数y1=x2+![]() x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
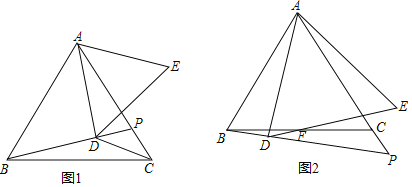
(3)已知函数y=![]() (x-2)(x+3)的图像与
(x-2)(x+3)的图像与![]() 轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=
轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=![]() (x-2)(x+3)互为“旋转函数”.
(x-2)(x+3)互为“旋转函数”.
【答案】(1) y=2x2+5x+3 ;(2)1;(3)见解析.
【解析】
(1)根据题目中的条件直接可以写出函数表达式(2)根据a1+a2=0,b1=b2,c1+c2=0的规律列出等式进行计算即可(3)函数y=![]() (x-2)(x+3)的图像与
(x-2)(x+3)的图像与![]() 轴交于A、B两点,与y轴交于点C,求出点的坐标,再求出关于原点的对称点,进而求出经过对称点的二次函数,通过“旋转函数”的规律就可以证明两函数是互为“旋转函数”.
轴交于A、B两点,与y轴交于点C,求出点的坐标,再求出关于原点的对称点,进而求出经过对称点的二次函数,通过“旋转函数”的规律就可以证明两函数是互为“旋转函数”.
(1) y=2x2+5x+3 ;
.(2)∵y1=x2+![]() x-n与y2=-x2-mx-2互为“旋转函数”,
x-n与y2=-x2-mx-2互为“旋转函数”,
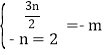 ∴解得
∴解得![]()
∴(m+n)2019=(3-2)2019 =1
(3)证明:当x=0时,y=![]() (x-2)(x+3),则C(0,-3),
(x-2)(x+3),则C(0,-3),
当y=0时,![]() (x-2)(x+3)=0,解得x1=2,x2=-3,则A(2,0),B(-3,0),
(x-2)(x+3)=0,解得x1=2,x2=-3,则A(2,0),B(-3,0),
∵点A、B、C关于原点的对称点分别是A1,B1,C1,
∴A1(-2,0),B1(3,0),C1(0,3),
可求过点A1,B1,C1的二次函数解析式为y=-![]() (x+2)(x-3)=-
(x+2)(x-3)=-![]() x2+
x2+![]() x+3…8分
x+3…8分
y=![]() (x-2)(x+3)=
(x-2)(x+3)=![]() x2+
x2+![]() x-3
x-3
∵a1+a2=![]() +(-
+(-![]() )=0,b1=b2=
)=0,b1=b2=![]() ,c1+c2=3+(-3)=0
,c1+c2=3+(-3)=0
∴经过点A1,B1,C1的二次函数与函数y=![]() (x-2)(x+3)互为“旋转函数”
(x-2)(x+3)互为“旋转函数”

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】抛物线y=ax2+bx+c上部分点的横坐标x和纵坐标y的对应值如下表,则下列说法中正确的有_______.(填序号)
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
①当x>1时,y随x的增大而减小. ②抛物线的对称轴为直线x=-![]() .
.
③当x=2时,y=-9. ④方程ax2+bx+c=0一个正数解![]() 满足1<
满足1<![]() <2.
<2.