题目内容
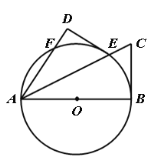
【题目】如图,D、E分别是⊙O两条半径OA、OB的中点,![]() .
.
(1)求证:CD=CE.
(2)若∠AOB=120°,OA=x,四边形ODCE的面积为y,求y与x的函数关系式.
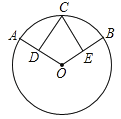
【答案】(1)证明见解析;(2)y=![]() x2.
x2.
【解析】
(1)连接OC,根据圆心角、弧、弦的关系定理得到∠COA=∠COB,证明△COD≌△COE,根据全等三角形的性质证明;
(2)连接AC,根据全等三角形的判定定理得到△AOC为等边三角形,根据正切的定义求出CD,根据三角形的面积公式计算即可.
(1)证明:连接OC,
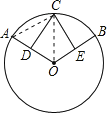
∵![]() ,
,
∴∠COA=∠COB,
∵D、E分别是⊙O两条半径OA、OB的中点,
∴OD=OE,
在△COD和△COE中,
 ,
,
∴△COD≌△COE(SAS)
∴CD=CE;
(2)连接AC,
∵∠AOB=120°,
∴∠AOC=60°,又OA=OC,
∴△AOC为等边三角形,
∵点D是OA的中点,
∴CD⊥OA,OD=![]() OA=
OA=![]() x,
x,
在Rt△COD中,CD=ODtan∠COD=![]() ,
,
∴四边形ODCE的面积为y=![]() ×OD×CD×2=
×OD×CD×2=![]() x2.
x2.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目