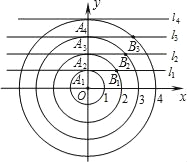
��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���A��ֱ��l�ϣ���AΪԲ�ģ�OAΪ�뾶��Բ��y�����һ������ΪE���������¶��壺���߶�OE����A��ֱ��l�Ϸֱ���ڵ�B����C�͵�D��ʹ���ı���ABCD�Ǿ��Σ���A��B��C��D˳ʱ�����У�����ƾ���ABCDΪֱ��l�ġ�λ�þ��Ρ���
���磬ͼ�еľ���ABCDΪֱ��l�ġ�λ�þ��Ρ���

��1������A��-1��2�����ı���ABCDΪֱ��x=-1�ġ�λ�þ��Ρ������D������Ϊ ��
��2������A��1��2������ֱ��y=kx+1��k��0���ġ�λ�þ��Ρ��������
��3������A��1��-3����ֱ��l�ġ�λ�þ��Ρ���������ֵΪ ����ʱ��D������Ϊ ��
���𰸡���1����-1��0������2��![]() ����3��5����3��-2����-1��-2����
����3��5����3��-2����-1��-2����
��������
��1��ֻ������¶��廭��ͼ�ξͿɽ�����⣻
��2������A��AF��y���ڵ�F������AO��AC����ͼ2�����ݵ�A��1��2����ֱ��y=kx+1�Ͽ����k����ֱ��y=x+1��y���ཻ�ڵ�G�������OG=1����FGA=45�㣬���ݹ��ɶ��������AG��AB��BC��ֵ���Ӷ��������λ�þ��Ρ�ABCD�����
��3���衰λ�þ��Ρ���һ���ڱ߳��ֱ�Ϊx��y������x2+y2=10���ɣ�x-y��2=x2+y2-2xy=10-2xy��0�ɵ�xy��5�����ҽ���x=yʱ��xyȡ���ֵ��5����ʱ��λ�þ��Ρ��������Σ�Ȼ��ֵ�D�ڵ������ޣ���ͼ3���͵������ޣ���ͼ4������������ۣ��Ϳɽ������
��1����ͼ1��
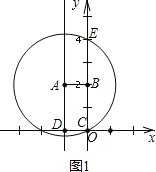
��D��������-1��0����
�ʴ�Ϊ��-1��0����
��2������A��AF��y���ڵ�F������AO��AC����ͼ2��
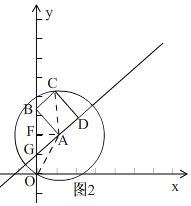
����A��������1��2����
��AC=AO=![]() ��AF=1��OF=2��
��AF=1��OF=2��
����A��1��2����ֱ��y=kx+1�ϣ�
��k+1=2��
���k=1��
��ֱ��y=x+1��y���ཻ�ڵ�G��
��x=0ʱ��y=1����G��0��1����OG=1��
��FG=OF-OG=2-1=1=AF��
���FGA=45�㣬AG=![]() ��
��
��Rt��GAB��AB=AGtan45��=![]() ��
��
��Rt��ABC��BC=![]() ��
��
������λ�þ��Ρ�ABCD���ΪABBC=![]() ��
��
��3���衰λ�þ��Ρ���һ���ڱ߳��ֱ�Ϊx��y��
����x2+y2=AC2=AO2=12+32=10��
����x-y��2=x2+y2-2xy=10-2xy��0��
��xy��5��
���ҽ���x=yʱ��xyȡ���ֵ��5����ʱ��λ�þ��Ρ��������Σ�
������D�ڵ�������ʱ����ͼ3��
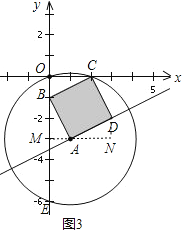
����A��x���ƽ���ߣ���y���ڵ�M��������Dƽ����y���ֱ���ڵ�N��
�ߡ�BAM+��DAN=90�㣬��BAM+��ABM=90�㣬
���ABM=��DAN��
��RtAMB��Rt��DNA��
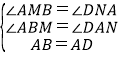 ��
��
��RtAMB��Rt��DNA��
����AN=BM=2��DN=AM=1��
����D��������1+2��-3+1������3��-2����
������D�ڵ�������ʱ����ͼ4��
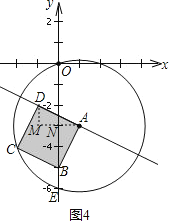
����A��x���ƽ���ߣ���y���ڵ�N��������Dƽ����y���ֱ���ڵ�M��
ͬ���ķ����ã�RtANB��Rt��DMA��
����DM=AN=1��AM=BN=2��
����D��������1-2��-3+1������-1��-2����
�ʴ�Ϊ��5����3��-2����-1��-2����