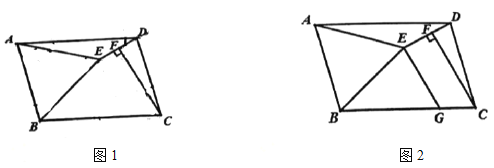题目内容
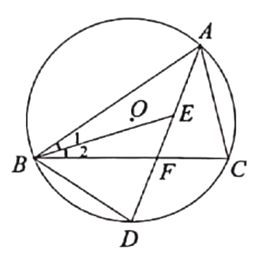
【题目】如图,△ABC内接于⊙O,∠ABC和 ∠BAC的平分线交于点E,延长AE分别交BC, ⊙O于点F, D,连接BD.
(1)求证: BD=DE.
(2)若BD=6,AD=10,求EF的长.
【答案】(1)证明见解析;(2)2.4.
【解析】
(1)根据角平分线的定义以及圆周角定理得到∠DBC=∠CAD,然后求出∠BED=∠BAD+∠1,∠DBE=∠DBC+∠2,得到∠BED=∠DBE即可;
(2)根据∠DBC=∠CAD=∠BAD,∠D=∠D,证得△DBF∽△DAB,利用相似三角形的性质列出比例式求出DF即可解决问题.
解:(1)∵AD 平分∠BAC,
∴∠BAD=∠CAD,
∴![]() =
=![]() ,
,
∴∠DBC=∠CAD,
∵BE 平分∠ABC,
∴∠1=∠2,
∵∠BED=∠BAD+∠1,∠DBE=∠DBC+∠2,
∴∠BED=∠DBE,
∴DB=DE;
(2)由(1)得∠DBC=∠CAD=∠BAD,
∵∠D=∠D,
∴△DBF∽△DAB,
∴![]() ,
,
∵BD=6,AD=10,
∴![]() ,
,
∴DF=3.6,
∵DE=BD=6,
∴EF=DE-DF=6-3.6=2.4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.