Question

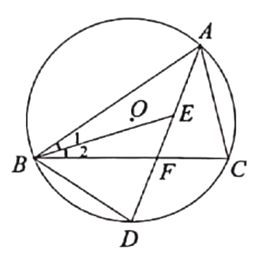
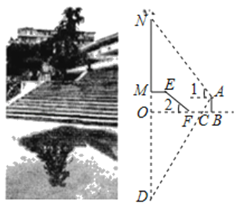
【题目】如图，雨后初睛，李老师在公园散步，看见积水水面上出现阶梯上方树的倒影，于是想利用倒影与物体的对称性测量这颗树的高度，他的方法是：测得树顶的仰角∠1、测量点A到水面平台的垂直高度AB、看到倒影顶端的视线与水面交点C到AB的水平距离BC．再测得梯步斜坡的坡角∠2和长度EF，根据以下数据进行计算，如图，AB＝2米，BC＝1米，EF＝4米，∠1＝60°，∠2＝45°．已知线段ON和线段OD关于直线OB对称．（以下结果保留根号）

（1）求梯步的高度MO；

（2）求树高MN．

Answer 1

【答案】（1）4米；（2）（14+4）米．

【解析】

（1）作EH⊥OB于H，由四边形MOHE是矩形，解Rt求得EH即可；

（2）设ON＝OD＝m，作AK⊥ON于K，则四边形AKOB是矩形，，OK＝AB＝2，想办法构建方程求得m即可.

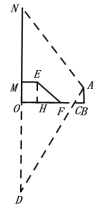
（1）如图，作EH⊥OB于H．则四边形MOHE是矩形．

∴OM＝EH，

在Rt中，

∵∠EHF＝90°，EF＝4，∠EFH＝45°，

∴EH＝FH＝OM＝米．

（2）设ON＝OD＝m．作AK⊥ON于K．则四边形AKOB是矩形，如图，

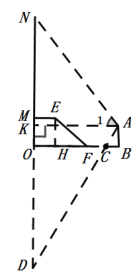
AK＝BO，OK＝AB＝2

∵AB∥OD，∴，∴，∴OC＝，

∴，

在Rt△AKN中，∵∠1＝60°，

∴AK，∴，

∴m＝（14+8）米，

∴MN＝ON﹣OM＝14+8﹣4＝（14+4）米．