题目内容
【题目】如图,四边形![]() 是平行四边形,
是平行四边形,![]() 是等边三角形,连接
是等边三角形,连接![]() ,
,![]() ,垂足为
,垂足为![]() .
.
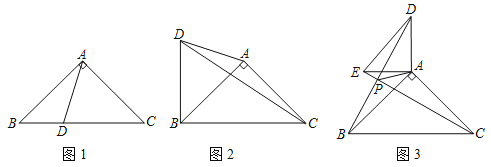
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
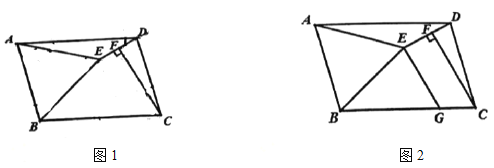
【答案】(1)30°;(2)证明见详解.
【解析】
(1)由四边形![]() 是平行四边形,
是平行四边形,![]() 是等边三角形,得∠BAE=60°,∠BAD+∠ADC=180°,从而得∠DAE+∠ADE+∠CDF=120°,结合
是等边三角形,得∠BAE=60°,∠BAD+∠ADC=180°,从而得∠DAE+∠ADE+∠CDF=120°,结合![]() ,
,![]() ,即可求解;
,即可求解;
(2)连接CE,在线段BG上截取BM=GC,易证CFECFD(SAS),得CD=CE,∠DCF=∠ECF,再证MBEGCE(SAS),得ME=GE,由∠ABE=60°,∠ABC+∠BCD=180°,得∠MBE+∠GCE+∠DCF+∠ECF=120°,从而得∠FCB=60°,易证CF∥GE,得∠EGM=∠FCB=60°,EMG是等边三角形,进而得GE=GM,即可得到结论.
(1)∵四边形![]() 是平行四边形,
是平行四边形,![]() 是等边三角形,
是等边三角形,
∴∠BAE=60°,∠BAD+∠ADC=180°,
∴∠DAE+∠ADE+∠CDF=180°-∠BAE=180°-60°=120°,
∵![]() ,
,
∴∠DCF+∠ADE+∠CDF=120°,
∵![]() ,
,
∴∠DCF+∠CDF=90°,
∴∠ADE=120°-(∠DCF+∠CDF)= 120°-90°=30°;
(2)连接CE,在线段BG上截取BM=GC,
∵![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
∴∠CFE=∠CFD=90°,EF=DF,
∵CF=CF,
∴CFECFD(SAS),
∴CD=CE,∠DCF=∠ECF,
∵四边形![]() 是平行四边形,
是平行四边形,![]() 是等边三角形,
是等边三角形,
∴CD=AB=BE,
∴CE=BE,
∴∠MBE=∠GCE,
在MBE和GCE中,
∵ ,
,
∴ MBEGCE(SAS),
∴ME=GE,
∵∠ABE=60°,∠ABC+∠BCD=180°,
∴∠MBE+∠BCD=180°-∠ABE=180°-60°=120°,
即:∠MBE+∠GCE+∠DCF+∠ECF=120°,
∴∠GCE+∠ECF=![]() ×120°=60°,即:∠FCB=60°,
×120°=60°,即:∠FCB=60°,
∵![]() ,
,
∴CF∥GE,
∴∠EGM=∠FCB=60°,
∴EMG是等边三角形,
∴GE=GM,
∴BG=GM+BM=GC+GE,即:![]() .
.


 阅读快车系列答案
阅读快车系列答案