题目内容
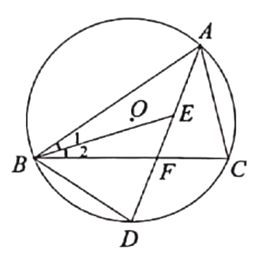
【题目】如图,△ABC中,AB=AC,AM为BC边的中线,点D在边AC上,联结BD交AM于点F,延长BD至点E,使得![]() =
=![]() ,联结CE.
,联结CE.
求证:(1)∠ECD=2∠BAM;
(2)BF是DF和EF的比例中项.
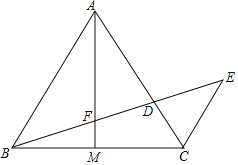
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)由等腰三角形的性质可得∠BAC=2∠BAM,通过证明△ADB∽△CDE,可得∠BAC=∠ECD=2∠BAM;
(2)由等腰三角形的性质可得BF=CF,通过证明△DCF∽△CEF,可得![]() ,可得结论.
,可得结论.
证明:(1)∵AB=AC,AM为BC边的中线,
∴∠BAC=2∠BAM,
∵![]() =
=![]() ,∠ADB=∠CDE,
,∠ADB=∠CDE,
∴△ADB∽△CDE,
∴∠BAC=∠ECD,
∴∠ECD=2∠BAM;
(2)如图,连接CF,

∵AB=AC,AM为BC边的中线,
∴AM是BC的垂直平分线,
∴BF=CF,且AB=AC,AF=AF,
∵△ABF≌△ACF(SSS)
∴∠ABF=∠ACF,
由(1)可知:△ADB∽△CDE,
∴∠ABF=∠E,
∴∠ACF=∠E,且∠EFC=∠DFC,
∴△DCF∽△CEF,
∴![]() ,且BF=CF,
,且BF=CF,
∴BF2=DFEF,
∴BF是DF和EF的比例中项.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目