题目内容
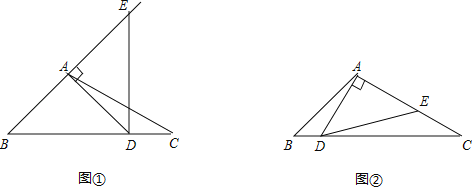
【题目】如图,在△ABC中,AC=BC,∠ACB=120°,D是AB中点,一个以点D为顶点的60°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
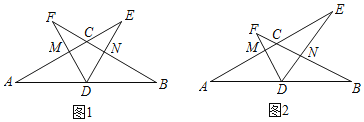
(1)如图1,若CE=CF,求证:DE=DF;
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AC,CE,CF之间的数量关系,并说明理由;
②若CE=9,CF=4,求CN的长.
【答案】(1)证明见解析(2)①见解析②![]()
【解析】
(1)证明△DCE≌△DCF(SAS),即可解决问题.
(2)①证明△CDF∽△CED,可得![]() ,即CD2=CECF,再证明AC=2CD即可解决问题.
,即CD2=CECF,再证明AC=2CD即可解决问题.
②作DK∥AE交BC于K.利用平行线分线段成比例定理即可解决问题.
(1)证明:如图1中,连接CD.
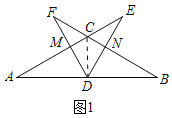
∵∠ACB=120°,AC=BC,AD=BD,
∴∠BCD=∠ACD=60°,∠BCE=∠ACF=60°.
∴∠DCE=∠DCF=120°.
又∵CE=CF,CD=CD,
∴△DCE≌△DCF(SAS),
∴DE=DF;
(2)①如图2中,连接CD.
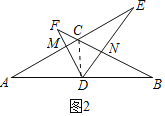
∵∠DCF=∠DCE=120°,
∴∠CDF+∠F=180°-120°=60°.
又∵∠CDF+∠CDE=60°,∴∠F=∠CDE.
∴△CDF∽△CED,
∴![]() ,即CD2=CECF.
,即CD2=CECF.
∵∠ACB=120°,AC=BC,AD=BD,
∴CD=![]() AC.
AC.
∴AC2=4CECF.
②作DK∥AE交BC于K.
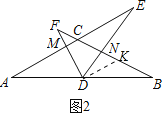
∵AC2=4CECF=144,
∴AC=BC=12,
∵AD=BD.DK∥AC,
∴CK=KB=6,
∴DK=![]() AC=6,
AC=6,
∵![]() ,
,
∴CN=![]() CK=
CK=![]() .
.

练习册系列答案
相关题目