Question

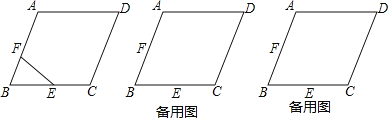
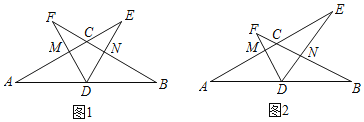
【题目】在△ABC中，∠B＝45°，∠C＝30°，点D是边BC上一点，连接AD，将线段AD绕点A逆时针旋转90°，得到线段AE，连接DE．

（1）如图①，当点E落在边BA的延长线上时，∠EDC＝　 　度（直接填空）；

（2）如图②，当点E落在边AC上时，求证：BD＝EC；

（3）当AB＝2，且点E到AC的距离等于﹣1时，直接写出tan∠CAE的值．

Answer 1

【答案】（1）90；（2）详见解析；（3）

【解析】

（1）利用三角形的外角的性质即可解决问题；

（2）如图2中，作PA⊥AB交BC于P，连接PE．只要证明△BAD≌△PAE（SAS），提出BD=PE，再证明EC=2PE即可；

（3）如图3，作EF⊥AC于F，延长FE交BC于H，作AG⊥BC于G，PA⊥AB交BC于P，连接PE．设PH＝x，在Rt△EPH中，可得EP＝x，EH＝2PH＝2x，

由此FH＝2x+﹣1，CF＝2x+3﹣，由△BAD≌△PAE，得BD＝EP＝x，AE＝AD，在Rt△ABG中， AG＝GB＝2，在Rt△AGC中，AC＝2AG＝4，故AE2＝AD2＝AF2+EF2，由勾股定理得AF＝1+，由此tan∠EAF＝2﹣，根据对称性可得tan∠EAC＝．

（1）如图1中，

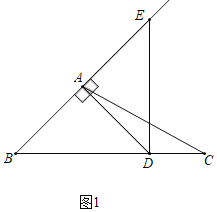
∵∠EDC＝∠B+∠BED，∠B＝∠BED＝45°，

∴∠EDC＝90°，

故答案为90；

（2）如图2中，作PA⊥AB交BC于P，连接PE．

∵∠DAE＝∠BAP＝90°，

∴∠BAD＝∠PAE，

∵∠B＝45°，

∴∠B＝∠APB＝45°，

∴AB＝AP，

∵AD＝AE，

∴△BAD≌△PAE（SAS），

∴BD＝PE，∠APE＝∠B＝45°，

∴∠EPD＝∠EPC＝90°，

∵∠C＝30°，

∴EC＝2PE＝2BD；

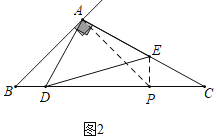
（3）如图3，作EF⊥AC于F，延长FE交BC于H，作AG⊥BC于G，PA⊥AB交BC于P，连接PE．

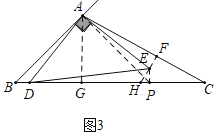
设PH＝x，在Rt△EPH中，∵∠EPH＝90°，∠EHP＝60°，

∴EP＝x，EH＝2PH＝2x，

∴FH＝2x+﹣1，CF＝FH＝2x+3﹣，

∵△BAD≌△PAE，

∴BD＝EP＝x，AE＝AD，

在Rt△ABG中，∵AB＝2，

∴AG＝GB＝2，

在Rt△AGC中，AC＝2AG＝4，

∵AE2＝AD2＝AF2+EF2，

∴22+（2﹣x）2＝（﹣1）2+（4﹣2x﹣3+）2，

整理得：9x2﹣12x＝0，

解得x＝（舍弃）或0

∴PH＝0，此时E，P，H共点，

∴AF＝1+，

∴tan∠EAF＝＝＝2﹣．

根据对称性可知当点E在AC的上方时，同法可得tan∠EAC＝．