题目内容
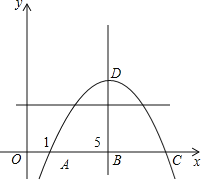
【题目】如图所示，抛物线L：y＝ax2+bx+c（a＜0）的对称轴为x＝5，且与x轴的左交点为(1，0)，则下列说法正确的有（ ）
①C(9，0)；②b+c＞﹣10；③y的最大值为﹣16a；④若该抛物线与直线y＝8有公共交点，则a的取值范围是a≤
．
A.①②③④B.①②③C.①③④D.①④
【答案】B
【解析】
利用抛物线的对称性求得抛物线与x轴的另一个交点坐标，从而判断①；
将（1,0）代入函数解析式求得a+b+c＝0，然后求得b+c＝﹣a＞0，从而判断②；
由抛物线的对称轴公式得b＝﹣10a，由a+b+c＝0得c＝9a，然后代入抛物线顶点纵坐标公式求解，从而判断③；
该抛物线与直线y＝8有公共交点，可知抛物线顶点位于直线y＝8上方，列不等式求解，从而判断④．
解：∵抛物线L：y＝ax2+bx+c（a＜0）的对称轴为x＝5，且与x轴的左交点为（1，0）
∴抛物线L与x轴的交点C为（9，0）
故①正确；
∵抛物线L与x轴的左交点为（1，0）
∴a+b+c＝0
∴b+c＝﹣a＞0＞﹣10
故②正确；
∵抛物线L：y＝ax2+bx+c（a＜0）的对称轴为x＝5
∴﹣
＝5，即b＝﹣10a
又∵a+b+c＝0
∴c＝9a
∴
＝
＝﹣16a
故③正确；
若该抛物线与直线y＝8有公共交点，则有8≤﹣16a，
∴a≤﹣
故④错误．
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
