��Ŀ����
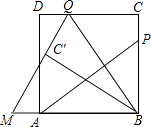
����Ŀ����ͼ����A��0�� ![]() ��ΪԲ�ĵ�Բ��x������������ԭ��O����y���ཻ�ڵ�B����BD���ӳ��߽�x��ĸ������ڵ�E���ҡ�BEO��60�㣬AD���ӳ��߽�x���ڵ�C��
��ΪԲ�ĵ�Բ��x������������ԭ��O����y���ཻ�ڵ�B����BD���ӳ��߽�x��ĸ������ڵ�E���ҡ�BEO��60�㣬AD���ӳ��߽�x���ڵ�C��
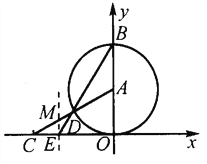
��1���ֱ����E��C�����ꣻ
��2����A��C���㣬���Թ�E��ƽ����y���ֱ��Ϊ�Գ���������ߵĺ�������ʽ��
��3���������ߵĶԳ�����AC�Ľ���ΪM�����ж���M��ΪԲ�ģ�MEΪ�뾶��Բ���A��λ�ù�ϵ����˵�����ɣ�
���𰸡���1����C������Ϊ����3��0����2��![]() ��3����M���A����
��3����M���A����
�������������������1����֪��A������꣬���ɵó�Բ�İ뾶��ֱ��������ֱ��������BOE�У�������BEO��OB�ij����OE�ij����������E������꣬ͬ������ֱ��������OAC�����C���������
��2����֪�˶Գ���Ľ���ʽ���ɾݴ����C����ڶԳ���ԳƵĵ�����꣬Ȼ����ݴ˵������Լ�C��A�������ô���ϵ����������������ߵĽ���ʽ��
��3����ԲӦ�����У�����ֱ��DE��OB�������MED=��ABD������AB=AD����ô��ADB=��ABD������ȵĽǽ����û���ɵó���MED=��MDE����ME=MD�������Բ��Բ�ľ�AM=ME+AD������Բ�İ뾶�ͣ������Բ����.
�����������1����Rt��EOB�� ![]() ��
��
���E����������2��0����
��Rt��COA�� ![]() ��
��
���C����������3��0����
��2���ߵ�C���ڶԳ���![]() �ԳƵĵ������ΪF����1��0����
�ԳƵĵ������ΪF����1��0����
����C���F����1��0�������������ϣ�
����![]() ����
����![]() �����
�����
![]() ��
��
��![]() ������
������
��![]() ����
����
![]() ��
��
��3����M���A���У�֤�����£�
��ME��y�ᣬ
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���M���A����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�