题目内容
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() ,
,![]() (或它们的延长线)于点
(或它们的延长线)于点![]() ,
,![]() 。当
。当![]() 绕点
绕点![]() 旋转到
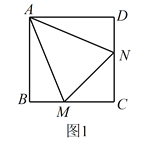
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .(不必证明)
.(不必证明)
(1)当![]() 绕点
绕点![]() 旋转到
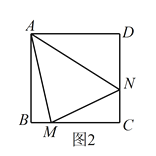
旋转到![]() 时(如图2),线段
时(如图2),线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明。
之间有怎样的数量关系?写出猜想,并加以证明。
(2)当![]() 绕点
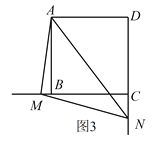
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() ,
,![]() 和
和![]() 之间又有怎样的数量关系?写出猜想,并加以证明。
之间又有怎样的数量关系?写出猜想,并加以证明。
【答案】(1)BM+DN=MN;(2)BM+DN=MN;(3)DN﹣BM=MN.
【解析】
(1)连接AC,交MN于点G,则可知AC垂直平分MN,结合∠MAN=45°,可证明△ABM≌△AGM,可得到BM=MG,同理可得到NG=DN,可得出结论;
(2)在MB的延长线上,截取BE=DN,连接AE,则可证明△ABE≌△ADN,可得到AE=AN,进一步可证明△AEM≌△ANM,可得结论BM+DN=MN;
(3)在DC上截取DF=BM,连接AF,可先证明△ABM≌△ADF,进一步可证明△MAN≌△FAN,可得到MN=NF,从而可得到DN﹣BM=MN
(1)如图1,连接AC,交MN于点G.
∵四边形ABCD为正方形,∴BC=CD,且BM=DN,∴CM=CN,且AC平分∠BCD,∴AC⊥MN,且MG=GN,∴∠MAG=∠NAG.
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,∴∠BAM=∠GAN=∠GAM.在△ABM和△AGM中,∵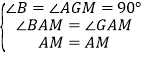 ,∴△ABM≌△AGM(AAS),∴BM=MG,同理可得GN=DN,∴BM+DN=MG+GN=MN,∴BM+DN=MN;
,∴△ABM≌△AGM(AAS),∴BM=MG,同理可得GN=DN,∴BM+DN=MG+GN=MN,∴BM+DN=MN;
(2)猜想:BM+DN=MN.证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE.在△ABE和△ADN中,∵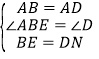 ,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,∴∠BAM+∠DAN=45°,∴∠EAB+∠BAM=45°,∴∠EAM=∠NAM.
在△AEM和△ANM中,∵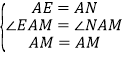 ,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
(3)DN﹣BM=MN.证明如下:
如图3,在DC上截取DF=BM,连接AF,△ABM和△ADF中,∵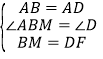 ,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即MAF=∠BAD=90°.
,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即MAF=∠BAD=90°.
∵∠MAN=45°,∴∠MAN=∠FAN=45°.
在△MAN和△FAN中,∵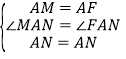 ,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.
,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.

 阅读快车系列答案
阅读快车系列答案