题目内容
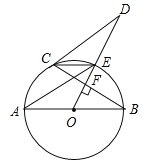
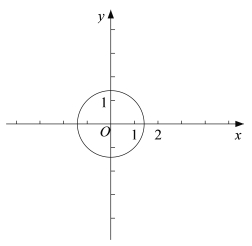
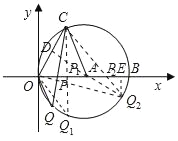
【题目】如图所示,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,P是x轴上的一动点,连接CP.
(1)直接写出OC=___________;
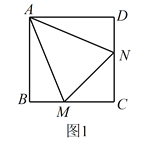
(2)如图1,当CP与⊙A相切时,求PO的长;
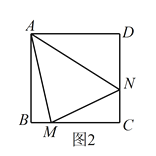
(3)如图2,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问当PO为何值时,△OCQ是等腰三角形?

【答案】(1)4;(2)4 (3)PO为2或2+2![]()
【解析】
(1)根据已知条件证明△AOC是等边三角形,由此即可求解;(2)根据切线的性质可得∠ACP=90°,在直角三角形APC中,即可得∠APC= 30°;有已知A点的坐标可得AC的长,即可求得PA的长,再由PO=PA-OA得出OP的值即可;(3)分OC=OQ和CQ=OQ两种情况求PO得值即可.
(1)∵∠AOC=60°,AO=AC,
∴△AOC是等边三角形,
∴OC=OA=4
(2)∵CP与⊙A相切,
∴∠ACP=90°,
∴∠APC=90°﹣∠OAC=30°;
又∵A(4,0),
∴AC=AO=4,
∴PA=2AC=8,
∴PO=PA﹣OA=8﹣4=4.
(3)①如图,过点C作CP1⊥OB,垂足为P1,延长CP1交⊙A于Q1;
∵OA是半径,
∴![]() ,
,
∴OC=OQ1,
∴△OCQ1是等腰三角形;
又∵△AOC是等边三角形,
∴P1O=![]() OA=2;
OA=2;
②如图,过A作AD⊥OC,垂足为D,延长DA交⊙A于Q2,CQ2与x轴交于P2,
∵A是圆心,
∴DQ2是OC的垂直平分线,
∴CQ2=OQ2,
∴△OCQ2是等腰三角形;
过点Q2作Q2E⊥x轴于E,
在Rt△AQ2E中,
∵∠Q2AE=∠OAD=![]() ∠OAC=30°,
∠OAC=30°,
∴Q2E=![]() AQ2=2,AE=2
AQ2=2,AE=2![]() ,
,
∴点Q2的坐标(4+![]() ,﹣2);
,﹣2);
在Rt△COP1中,
∵P1O=2,∠AOC=60°,
∴![]() ,
,
∴C点坐标(2,![]() );
);
设直线CQ2的关系式为y=kx+b,则
![]() ,
,
解得![]() ,
,
∴y=﹣x+2+2![]() ;
;
当y=0时,x=2+2![]() ,
,
∴P2O=2+2![]() ,
,
即:PO为2或2+2![]() 时,△OCQ是等腰三角形.
时,△OCQ是等腰三角形.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案