题目内容
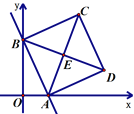
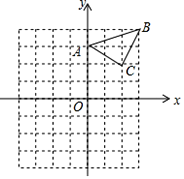
【题目】如图,在平面直角坐标系中,在边长为![]() 个单位长度的小正方形组成的方格中,点
个单位长度的小正方形组成的方格中,点![]() 都在格点上.
都在格点上.
(1)画出ΔABC绕着点B逆时针旋转90°得到的ΔA'B'C',并写出的A'的坐标__________
(2)在(1)的情况下,直接写出线段AA’的长度____________.
(3)在y轴上找一点P,使ΔPAB的周长最小,直接写出P的坐标_____________.

【答案】(1)作图见解析,A'的坐标(﹣3,3);(2)![]() ;(3)P(0,
;(3)P(0,![]() ).
).
【解析】
(1)根据题意画出相应的三角形,确定出所求点坐标即可;
(2)根据勾股定理求出AA′的长度即可;
(3)作A关于y轴的对称点D,连接BD交y轴于点P.连接AP,则△ABP的周长最小,由B、D的坐标求出直线BD的解析式,令x=0,即可得到y的值,从而得到P的坐标.
(1)画出ΔABC绕着点B逆时针旋转90°得到的ΔA'B'C',A'的坐标(﹣3,3);
(2)连接AA′,在直角三角形ABC中,AB2=BC2+AC2=22+42=20.
∵A′B′=AB,AA′=![]() .
.
故答案为:![]() ;
;
(3)作A关于y轴的对称点D,连接BD交y轴于点P.连接AP,则△ABP的周长最小.
∵B(-5,-1),D(1,-3).设直线BD为y=kx+b,则![]() ,解得:
,解得: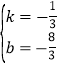 ,∴
,∴![]() ,当x=0时,y=
,当x=0时,y=![]() ,∴P(0,
,∴P(0,![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】下表是三种电话计费方式:
月使用费 (元) | 主叫限定时间 (分钟) | 主叫超时收费 (元/分钟) | 被叫 | |
方式一 | 18 | 60 | 0.2 | 免费 |
方式二 | 28 | 120 | 0.2 | 免费 |
方式三 | 48 | 240 | 0.2 | 免费 |
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费.
设一个月内主叫通话![]() 分钟(
分钟(![]() 为正整数).
为正整数).
(1)当![]() 时,按方式一计费为______元;按方式二计费为______元.
时,按方式一计费为______元;按方式二计费为______元.
(2)当![]() 时,是否存在某一时间
时,是否存在某一时间![]() ,使方式二与方式三的计费结果相等?若存在,请求出对应的值,若不存在,请说明理由.
,使方式二与方式三的计费结果相等?若存在,请求出对应的值,若不存在,请说明理由.
(3)当![]() 时,哪一种收费方式最省钱?请说明理由.
时,哪一种收费方式最省钱?请说明理由.