题目内容
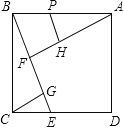
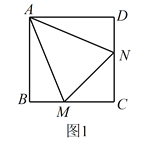
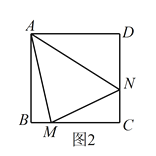
【题目】如图1,矩形ABCD中,点E是边AD上动点,点F是边BC上动点,连接EF,把矩形ABCD沿直线EF折叠,点B恰好落在边AD上,记为点G;如图2,把矩形展开铺平,连接BE,FG.

(1)判断四边形BEGF的形状一定是 ,请证明你的结论;
(2)若矩形边AB=4,BC=8,直接写出四边形BEGF面积的最大值为 .
【答案】(1)四边形BEGF是菱形,证明见解析;(2)四边形BEGF面积的最大值为20.
【解析】
(1)由折叠的性质可得∠BFE=∠EFG,BF=FG,由平行线的性质可得∠DEF=∠GFE=∠EFB,可得EG=FG=BF,AD∥BC,可证四边形BEGF是菱形;
(2)当EG最大时,四边形BEGF面积有最大值,由勾股定理可求EG的长,即可求解.
(1)四边形BEGF是菱形,
∵四边形ABCD是矩形
∴AD∥BC,
∴∠DEF=∠EFB,
∵把矩形ABCD沿直线EF折叠,点B恰好落在边AD上,
∴∠BFE=∠EFG,BF=FG,
∴∠DEF=∠GFE,
∴EG=FG,
∴EG=BF,且AD∥BC,
∴四边形BEGF是平行四边形,且BF=FG,
∴四边形BEGF是菱形,
(2)∵四边形BEGF是菱形,
∴BE=EG,
∵S四边形BEGF=EG×AB=4EG,
∴当EG最大时,四边形BEGF面积有最大值,
当AE+EG=AD时,EG最大,
∵AB2+AE2=BE2,
∴![]() ,
,
∴![]() ,
,
∴BE=5=EG,
∴四边形BEGF面积的最大值=4×5=20.

练习册系列答案
相关题目