题目内容
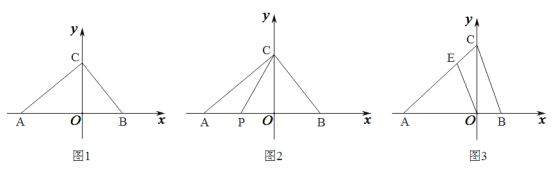
【题目】如图1，在平面直角坐标系中，
，
在
轴上，
在
轴上，
.
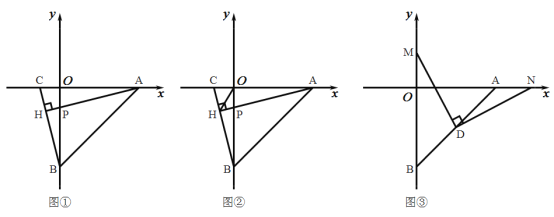
（1）求证：
；
（2）如图2，若点
，
，现有一个动点
从点出发，沿着轴正方向运动，连结
，当
为等腰三角形时，求点的坐标；
（3）如图3，若
，点
，过
作
交
于
，求
的长.
【答案】（1）详见解析；（2）满足条件的点
有四个，分别为：
，
，
，
；（3）
.
【解析】
(1)利用勾股定理即可证明.
(2)先由勾股定理算出B的坐标,再分类讨论等腰三角形可能的情况.
(3)取OE中点F,连接AF,证明
,即可利用条件算出OE.
（1）∵
∴
∵
∴
（2）∵
，
∴
，
∴
即
为等腰三角形时，可分为以下三种情况讨论：
若
时，
即点距离点
有5个单位
∴
或者
若
时，则点为点关于
轴的对称点
∴
若
时，可设
，则
由
可解得
∴
综上所述，满足条件的点有四个，分别为：，，，.
（3）∵
∴
∵
∴
∴
为以
为底的等腰三角形
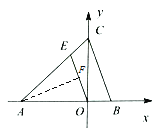
取的中点
，连结
则
，即
在
与
中
∴
∴
∴
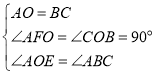
练习册系列答案
相关题目
