题目内容
【题目】如图所示,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
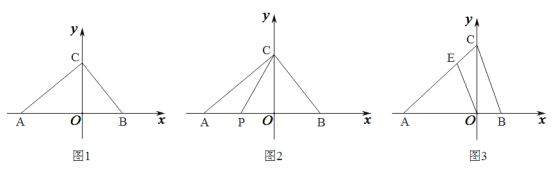
(1)如图①,若![]() 的坐标为
的坐标为![]() ,且
,且![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,试求点
,试求点![]() 的坐标;
的坐标;
(2)如图②,在(I)的条件下,连接![]() ,求
,求![]() 的度数;
的度数;
(3)如图③,若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() 点,当
点,当![]() 点在
点在![]() 轴正半轴上运动的过程中,式子
轴正半轴上运动的过程中,式子![]() 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
【答案】(1)![]() ;(2)45°;(3)
;(2)45°;(3)![]() 的值不发生改变,等于4,理由详见解析.
的值不发生改变,等于4,理由详见解析.
【解析】
(1)由余角的性质,可得:![]() ,从而证明:
,从而证明:![]() ,进而求出点P的坐标;
,进而求出点P的坐标;
(2)过![]() 分别作
分别作![]() 于
于![]() 点,作
点,作![]() 于
于![]() 点,易证:
点,易证:![]() ,可得:
,可得:![]() ,从而可得:
,从而可得:![]() 平分
平分![]() ,即可得到答案;
,即可得到答案;
(3)连接![]() ,易证:
,易证:![]() ,
,![]() ,
,![]() ,进而可证:
,进而可证:![]() ,得到:
,得到:![]() ,即
,即![]()
![]()
![]() ,即可得到结论.
,即可得到结论.
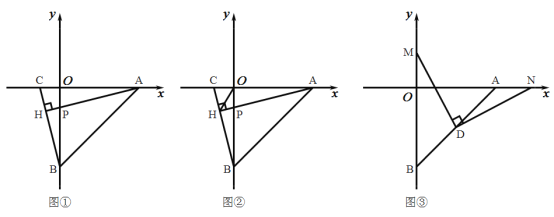
(1)如图1,由题意,![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
∵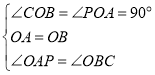
∴![]()
∴![]() ,即:
,即:![]() ;
;
(2)过![]() 分别作
分别作![]() 于
于![]() 点,作
点,作![]() 于
于![]() 点,如图2,
点,如图2,
∵在四边形![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
∵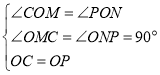 ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() 平分
平分![]() ,
,
∴![]() ;
;
(3)![]() 的值不发生改变,等于4. 理由如下:
的值不发生改变,等于4. 理由如下:
连接![]() ,如图3,
,如图3,
∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
∵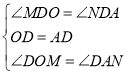 ,
,
∴![]() .
.
∴![]() ,
,
∴![]()
![]()
![]() .
.

练习册系列答案
相关题目