题目内容
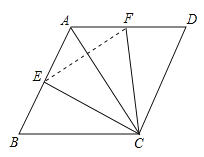
【题目】如图,△ABC和△ADC都是等边三角形,点E,F同时分别从点B,A出发,以相同的速度各自沿BA,AD的方向运动到点A,D停止,连结EC,FC.

(1)在点E,F运动的过程中,∠ECF的大小是否随之变化?请说明理由.
(2)在点E,F运动的过程中,以A,E,C,F为顶点的四边形的面积变化了吗?请说明理由.
(3)连结EF,在图中找出所有和∠ACE相等的角,并说明理由.
(4)若点E,F在射线BA,射线AD上继续运动下去,(1)中的结论还成立吗?直接写出结论,不必说明理由.
【答案】(1)没有变化(2)没有变化(3)∠AFE=∠DCF=∠ACE(4)(1)中的结论仍成立
【解析】试题分析:(1)由于BE=AF,BC=AC,且∠B=∠CAF=60°,根据SAS可证得△BCE≌△ACF,即可得∠BCE=∠ACF,因此∠ECF=∠ACF+∠ACE=∠BCE+∠ACE=60°,因此∠ECF的度数是定值,不会改变.(2)由(1)的全等三角形知:△ACF、△BCE的面积相等,因此四边形AECF的面积可转化为△ABC的面积,因此当E、F分别在线段AB、AD上运动时,四边形AECF的面积不变.(3)同(1)可证得△ACE≌△DCF,得∠ACE=∠FCD;连接EF,由(1)(3)的全等三角形,易知CE=CF,且∠ECF=60°,因此△ECF是等边三角形,那么∠EFC=60°,然后根据平角的定义以及三角形内角和定理,证得∠AFE=∠FCD,进而可求得∠ACE相等的角是:∠ACE=∠AFE=∠FCD.(4)由于当E、F分别在BA、AD延长线上时,(1)的全等三角形依然成立,因此(1)的结论是成立的.
试题解析:
(1)没有变化.理由如下:
∵点E,F的速度相同,且同时运动,
∴BE=AF.
∵△ABC和△ADC都是等边三角形,
∴BC=AC,∠B=∠ACB=∠CAF=60°.
在△BCE和△ACF中,∵ 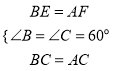
∴△BCE≌△ACF(SAS).∴∠BCE=∠ACF.
∴∠ECF=∠ACF+∠ACE=∠BCE+∠ACE=∠ACB=60°.
(2)没有变化.理由如下:
由(1)知,△BCE与△ACF的面积相等,
∴S四边形AECF=S△ACF+S△ACE=S△BCE+S△ACE=S△ABC.
∴四边形AECF的面积没有变化.
(3)∠AFE=∠DCF=∠ACE.理由如下:
∵△ABC和△ADC都是等边三角形,
∴∠EAC=∠FDC=60°,AB=AC=DC=AD.
∵BE=AF,∴AB-BE=AD-AF,即AE=DF.
∴△ACE≌△DCF(SAS).
∴∠ACE=∠DCF,EC=FC.
又∵∠ECF=60°,
∴△ECF是等边三角形,∴∠EFC=60°.
∴∠AFE+∠DFC=120°.
∵∠D=60°,∴∠DCF+∠DFC=120°.
∴∠AFE=∠DCF=∠ACE.
(4)(1)中的结论仍成立.

【题目】某人去水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.B家的规定如下表:
数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
[表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100﹣1500)]
(1)如果他批发600千克苹果,则他在A 家批发需要元,在B家批发需要元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要元,在B家批发需要元(用含x的代数式表示);
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.