题目内容
【题目】如图，D，E分别是AB，AC上的点，BE与CD交于点F，给出下列三个条件：①∠DBF=∠ECF；②∠BDF=∠CEF； ③BD=CE．两两组合在一起，共有三种组合：（1）①②；（2）①③；（3）②③问能判定AB=AC的组合的是（ ）
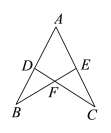
A.（1）（2）B.（1）（3）C.（2）（3）D.（1）（2）（3）
【答案】C
【解析】
由图形得出∠A=∠A，再依据所给条件进行判断△ABE≌△ACD即可得出结论.
∵∠DBF=∠ECF；∠BDF=∠CEF；∠A=∠A；
∴不能判断△ABE与△ACD全等，
∴（1）①②不能判定AB=AC；
在△BDF和△CEF中，
∠DBF=∠ECF，∠DFB=∠EFC，BD=CE，
∴△BDF≌△CEF
∴BF=CF，DF=EF，
∴BF+EF=CF+DF，即BE=CD,
在△ABE和△ACD中，
∠A=∠A，∠ABE=∠ACD，BE=CD，
∴△ABE≌△ACD，
∴AB=AC，
∴（2）①③能判断出AB=AC；
在△BDF和△CEF中，
∠BDF=∠CEF，∠DFB=∠EFC，BD=CE，
∴△BDF≌△CEF
∴BF=CF，DF=EF，
∴BF+EF=CF+DF，即BE=CD,
在△ABE和△ACD中，
∠A=∠A，∠ABE=∠ACD，BE=CD，
∴△ABE≌△ACD，
∴AB=AC，
∴（3）②③能判断出AB=AC.
故选：C.
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
