Question

【题目】如图，在三角形ABC中，∠C＝90°，AC＝6cm，BC＝10cm，点P从B点开始向C点运动速度是每秒1cm，设运动时间是t秒，

（1）用含t的代数式来表示三角形ACP的面积．

（2）当三角形ACP的面积是三角形ABC的面积的一半时，求t的值，并指出此时点P在BC上的什么位置？

Answer 1

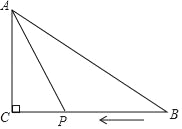
【答案】（1）三角形ACP的面积为30﹣3t；（2）此时BP=5，点P在BC的中点上．

【解析】

根据运动时间和速度表示出运动路程,即可求出面积.

（1）点P运动t秒后,BP=t,则PC=10﹣t,

三角形ACP的面积为：×PC×AC=×（10﹣t）×6=30﹣3t；

（2）因为三角形ABC的面积为：×BC×AC=×10×6=30,

依题意得 30﹣3t=30×,

解得,t=5,

此时BP=5,点P在BC的中点上．