题目内容
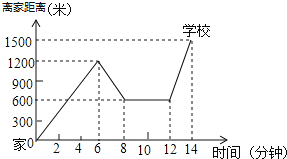
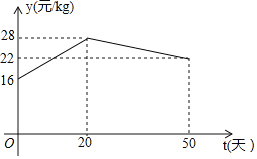
【题目】随着龙虾节的火热举办，某龙虾养殖大户为了发挥技术优势，一次性收购了10000kg小龙虾，计划养殖一段时间后再出售．已知每天养殖龙虾的成本相同，放养10天的总成本为166000，放养30天的总成本为178000元．设这批小龙虾放养t天后的质量为akg，销售单价为y元/kg，根据往年的行情预测，a与t的函数关系为a=
，y与t的函数关系如图所示．
（1）设每天的养殖成本为m元，收购成本为n元，求m与n的值；
（2）求y与t的函数关系式；
（3）如果将这批小龙虾放养t天后一次性出售所得利润为W元．问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大？最大利润是多少？
（总成本=放养总费用+收购成本；利润=销售总额﹣总成本）
【答案】（1）m=600，n=160000；（2）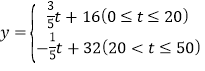
；（3）该龙虾养殖大户将这批小龙虾放养25天后一次性出售所得利润最大，最大利润是108500元.
【解析】（1）根据题意列出方程组，求出方程组的解得到m与n的值即可；
（2）根据图象，分类讨论利用待定系数法求出y与P的解析式即可；
（3）根据W=ya﹣mt﹣n，表示出W与t的函数解析式，利用一次函数与二次函数的性质求出所求即可．
（1）依题意得
，
解得：
；
（2）当0≤t≤20时，设y=k1t+b1，
由图象得：
，
解得：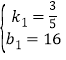
∴y=
t+16；
当20＜t≤50时，设y=k2t+b2，
由图象得：
，
解得：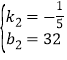
，
∴y=﹣
t+32，
综上，
；
（3）W=ya﹣mt﹣n，
当0≤t≤20时，W=10000（t+16）﹣600t﹣160000=5400t，
∵5400＞0，
∴当t=20时，W最大=5400×20=108000，
当20＜t≤50时，W=（﹣t+32）（100t+8000）﹣600t﹣160000=﹣20t2+1000t+96000=﹣20（t﹣25）2+108500，
∵﹣20＜0，抛物线开口向下，
∴当t=25，W最大=108500，
∵108500＞108000，
∴当t=25时，W取得最大值，该最大值为108500元．
