题目内容
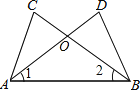
【题目】如图,△ABC中,AD⊥BC于D,若BD=AD,FD=CD.
(1)求证:∠FBD=∠CAD;
(2)求证:BE⊥AC.

【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)求出∠ADC=∠BDF=90°,根据SAS证△ADC≌△BDF,根据全等三角形的性质推出∠FBD=∠CAD即可;
(2)根据三角形的内角和定理求出∠FBD+∠BFD=90°,推出∠AFE+∠EAF=90°,在△AFE中,根据三角形的内角和定理求出∠AEF即可.
(1)∵AD⊥BC,
∴∠ADC=∠BDF=90°,
∵在△ADC和△BDF中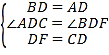 ,
,
∴△ADC≌△BDF(SAS),
∴∠FBD=∠CAD;
(2)∵∠BDF=90°,
∴∠FBD+∠BFD=90°,
∵∠AFE=∠BFD,由(1)知:∠FBD=∠CAD,
∴∠CAD+∠AFE=90°,
∴∠AEF=180°﹣(∠CAD+∠AFE)=90°,
∴BE⊥AC.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目