题目内容
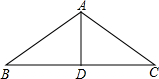
已知：梯形ABCD中，DC∥AB，∠A=36°，∠B=54°，M，N分别是DC，AB的中点．
求证：MN=
(AB-CD)．
求证：MN=
| 1 |
| 2 |
证明：如图，作DE∥CB，
∵∠A=36°，∠B=54°，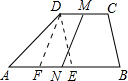
∴△ADE是直角三角形，其中AE=AB-CD，∠ADE=90°，
取AE中点F，连DF，则 FN=AN-AF=
-
=
，
∴FN∥DM且FN=DM，
∴DMNF是平行四边形，
∴DF=MN，
∵DF是直角△ADE斜边的中线，
∴2DF=AE=AB-CD，
∴2MN=AB-CD，
∴MN=
(AB-CD)．
∵∠A=36°，∠B=54°，
∴△ADE是直角三角形，其中AE=AB-CD，∠ADE=90°，
取AE中点F，连DF，则 FN=AN-AF=
| AB |
| 2 |
| AB-CD |
| 2 |
| CD |
| 2 |
∴FN∥DM且FN=DM，
∴DMNF是平行四边形，
∴DF=MN，
∵DF是直角△ADE斜边的中线，
∴2DF=AE=AB-CD，
∴2MN=AB-CD，
∴MN=
| 1 |
| 2 |
练习册系列答案
阅读快车系列答案
相关题目
