题目内容
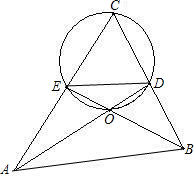
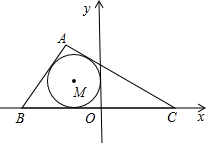
如图,△ABC的内切圆的圆心是M(-1,1),B(-1-
,0),C(1+
,0),则△ABC的面积S的值是______.
| 3 |
| 3 |

连接BE,
∵圆M切AC于E,切BC于F,切AB于W,切Y轴于N,
∴BW=BF,EQ=EN,
则BE过M,
∵M(-1,1),B(-1-
,0),C(1+
,0),
∴BF=1+
-1=
,MF=1,
由勾股定理得:BM=2,
∴MF=
BM,
∴∠EBC=30°,
∴∠ABC=60°,
∵X轴⊥Y轴,
∵OC=OB=1+
,
∴EB=EC,
∴∠ACB=∠ABC=30°,
∴∠A=180°-∠B-∠C=90°,
∴AB=
BC=
×(2+2
)=1+
,
由勾股定理得:AC=3+
,
∴三角形ABC的面积是
AC×AB=
×(1+
)×(3+
)=3+2
.
故答案为:3+2
.

∵圆M切AC于E,切BC于F,切AB于W,切Y轴于N,
∴BW=BF,EQ=EN,
则BE过M,
∵M(-1,1),B(-1-
| 3 |
| 3 |
∴BF=1+
| 3 |
| 3 |
由勾股定理得:BM=2,
∴MF=
| 1 |
| 2 |
∴∠EBC=30°,
∴∠ABC=60°,
∵X轴⊥Y轴,
∵OC=OB=1+
| 3 |
∴EB=EC,
∴∠ACB=∠ABC=30°,
∴∠A=180°-∠B-∠C=90°,
∴AB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
由勾股定理得:AC=3+
| 3 |
∴三角形ABC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
故答案为:3+2
| 3 |


练习册系列答案
相关题目