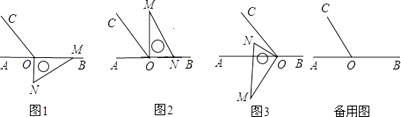题目内容
【题目】（本题满分10分）（1）问题发现
如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE，
填空：①∠AEB的度数为 ；
②线段AD、BE之间的数量关系是 ．
（2）拓展探究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=900， 点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由．
（3）解决问题如图3，在正方形ABCD中，CD=
．若点P满足PD=1，且∠BPD=900，请直接写出点A到BP的距离．
【答案】（1）①60；②AD=BE；（2）∠AEB＝900；AE=2CM+BE，理由见试题解析；（3）
或
．
【解析】
试题分析：（1）由条件易证△ACD≌△BCE，从而得到：AD=BE，∠ADC=∠BEC．由点A，D，E在同一直线上可求出∠ADC，从而可以求出∠AEB的度数．
（2）仿照（1）中的解法可求出∠AEB的度数，证出AD=BE；由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME，从而证到AE=2CH+BE．
（3）由PD=1可得：点P在以点D为圆心，1为半径的圆上；由∠BPD=90°可得：点P在以BD为直径的圆上．显然，点P是这两个圆的交点，由于两圆有两个交点，接下来需对两个位置分别进行讨论．然后，添加适当的辅助线，借助于（2）中的结论即可解决问题．
试题解析：（1）①如图1，
∵△ACB和△DCE均为等边三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=60°．∴∠ACD=∠BCE．
在△ACD和△BCE中，∵AC=BC，∠ACD=∠BCE，CD=CE，
∴△ACD≌△BCE（SAS），∴∠ADC=∠BEC．
∵△DCE为等边三角形，∴∠CDE=∠CED=60°．
∵点A，D，E在同一直线上，∴∠ADC=120°，∴∠BEC=120°，∴∠AEB=∠BEC﹣∠CED=60°．
故答案为：60°．
②∵△ACD≌△BCE，∴AD=BE．故答案为：AD=BE．
（2）∠AEB=90°，AE=BE+2CM．
理由：如图2，
∵△ACB和△DCE均为等腰直角三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=90°，∴∠ACD=∠BCE．
在△ACD和△BCE中，∵CA=CB，∠ACD=∠BCE，CD=CE，∴△ACD≌△BCE（SAS），
∴AD=BE，∠ADC=∠BEC．
∵△DCE为等腰直角三角形，∴∠CDE=∠CED=45°．
∵点A，D，E在同一直线上，∴∠ADC=135°，∴∠BEC=135°，∴∠AEB=∠BEC﹣∠CED=90°．
∵CD=CE，CM⊥DE，∴DM=ME，
∵∠DCE=90°，∴DM=ME=CM，∴AE=AD+DE=BE+2CM．
（3）∵PD=1，∴点P在以点D为圆心，1为半径的圆上．
∵∠BPD=90°，∴点P在以BD为直径的圆上，∴点P是这两圆的交点．
①当点P在如图3①所示位置时，
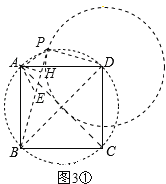
连接PD、PB、PA，作AH⊥BP，垂足为H，
过点A作AE⊥AP，交BP于点E，如图3①．
∵四边形ABCD是正方形，∴∠ADB=45°．AB=AD=DC=BC=
，∠BAD=90°，∴BD=2．
∵DP=1，∴BP=
．
∵A、P、D、B四点共圆，∴∠APB=∠ADB=45°，∴△PAE是等腰直角三角形．
又∵△BAD是等腰直角三角形，点B、E、P共线，AH⊥BP，∴由（2）中的结论可得：BP=2AH+PD．
∴=2AH+1，∴AH=
；
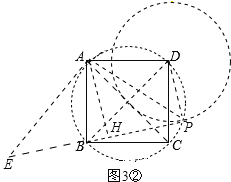
②当点P在如图3②所示位置时，
连接PD、PB、PA，作AH⊥BP，垂足为H，
过点A作AE⊥AP，交PB的延长线于点E，如图3②．
同理可得：BP=2AH﹣PD，∴=2AH﹣1，∴AH=．
综上所述：点A到BP的距离为或．
