题目内容
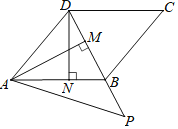
【题目】如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，DN＝3
，在DB的延长线上取一点P，满足∠ABD＝∠MAP+∠PAB，则AP＝（ ）
A.4.5B.5.5C.6D.6.5
【答案】C
【解析】
根据BD＝CD，AB＝CD，可得BD＝AB，再根据AM⊥BD，DN⊥AB，即可得到DN＝AM＝3
，依据∠ABD＝∠MAP+∠PAB，∠ABD＝∠P+∠PAB，即可得到△APM是等腰直角三角形，进而得到AP＝AM＝6．
解：∵四边形ABCD为平行四边形，
∴AB＝CD，
∵BD＝CD，
∴BD＝AB，
又∵AM⊥BD，DN⊥AB，
∴DN＝AM＝3，
又∵∠ABD＝∠MAP+∠PAB，∠ABD＝∠P+∠PAB，
∴∠P＝∠PAM，
∴△APM是等腰直角三角形，
∴AP＝AM＝6．
故选：C．
【题目】采用东阳南枣通过古法熬制而成的蜜枣是我们东阳的土特产之一，已知蜜枣每袋成本10元.试销后发现每袋的销售价
（元）与日销售量
（袋）之间的关系如下表：
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
若日销售量是销售价的一次函数，试求：
（1）日销售量（袋）与销售价（元）的函数关系式.
（2）要使这种蜜枣每日销售的利润最大，每袋的销售价应定为多少元？每日销售的最大利润是多少元？
【题目】某市扶贫办在精准扶贫工作中，组织30辆汽车装运花椒、核桃、甘蓝向外地销售．按计划30辆车都要装运，每辆汽车只能装运同一种产品，且必须装满，根据下表提供的信息，解答以下问题：
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量（吨） | 10 | 6 | 4 |
每吨土特产利润（万元） | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆，装运甘蓝的车辆数是装运核桃车辆数的2倍多1，假设30辆车装运的三种产品的总利润为y万元．
(1)求y与x之间的函数关系式；
(2)若装花椒的汽车不超过8辆，求总利润最大时，装运各种产品的车辆数及总利润最大值．
