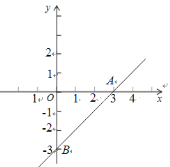题目内容
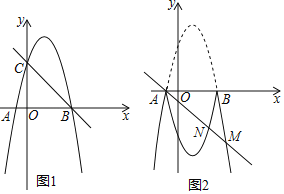
【题目】如图1,二次函数y=ax2﹣3ax+c的图象与x轴交于点A、B,与y轴交于点c直线y=﹣x+4经过点B、C.
(1)求抛物线的表达式;
(2)过点A的直线y=kx+k交抛物线于点M,交直线BC于点N,连接AC,当直线y=kx+k平分△ABC的面积,求点M的坐标;
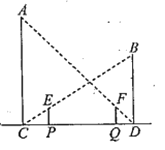
(3)如图2,把抛物线位于x轴上方的图象沿x轴翻折,当直线y=kx+k与翻折后的整个图象只有三个交点时,求k的取值范围.
【答案】(1)y=﹣x2+3x+4;(2)M(![]() ,
,![]() );(3)k的取值范围是﹣5<k<0.
);(3)k的取值范围是﹣5<k<0.
【解析】
(1)由直线y=-x+4知:点B、C的坐标分别为(4,0)、(0,4),则二次函数表达式为:y=ax2-3ax+4,将点A的坐标代入上式,即可求解;
(2)求出A的坐标,过点N作NG⊥AB于G,则根据直线y=kx+k平分△ABC的面积有![]() ,即可求出N的坐标,从而求出直线AM的解析式,再与抛物线解析式联立方程即可求M的坐标;
,即可求出N的坐标,从而求出直线AM的解析式,再与抛物线解析式联立方程即可求M的坐标;
(3)根据翻折的现在知翻折部分的函数表达式是![]() ,根据翻折的部分图象只有一个交点,则联立方程后判别式为零即可.
,根据翻折的部分图象只有一个交点,则联立方程后判别式为零即可.
(1)由直线y=﹣x+4知,点B、C的坐标分别为(4,0)、(0,4),
把点B、C的坐标分别为(4,0)、(0,4),
代入y=ax2﹣3ax+c,得![]() 解得
解得![]()
∴抛物线的表达式为:y=﹣x2+3x+4
(2)由y=﹣x2+3x+4,求得A(﹣1,0)
过点N作NG⊥AB于G,
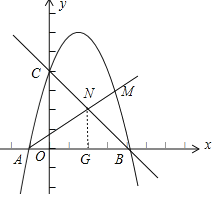
∵直线y=kx+k平分△ABC的面积,
∴![]() ,
,
∴当x=2时,2=﹣x+4,∴x=2
∴N(2,2)
把N(2,2)代入y=kx+k,得![]() ,
,
∴直线AM的解析式为![]() ,
,
由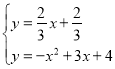 解得
解得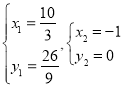
∴![]()
(3)翻折部分的函数表达式是![]()
当直线y=kx+k与翻折后的图象![]() 只有一个交点时,
只有一个交点时,
由![]() ,得x2﹣3x﹣4=kx+k,
,得x2﹣3x﹣4=kx+k,
整理,得x2﹣(k+3)x﹣(k+4)=0
△=[﹣(k+3)]2﹣4×[﹣(k+4)]=k2+10k+25=0
解得k1=k2=﹣5
∴当直线y=kx+k与翻折后的整个图象只有三个交点时,k的取值范围是﹣5<k<0.

 名校课堂系列答案
名校课堂系列答案【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元,经调查发现每天的销售量![]() (个
(个![]() 与每个商品的售价
与每个商品的售价![]() (元
(元![]() 满足一次函数关系,其部分数据如下所示:
满足一次函数关系,其部分数据如下所示:
每个商品的售价 |
| 30 | 40 | 50 |
|
每天销售量 |
| 100 | 80 | 60 |
|
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?