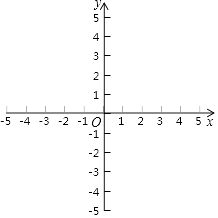题目内容
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG. 
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG; 
(2)如图3,如果α=45°,AB=2,AE=4 ![]() ,求点G到BE的距离.
,求点G到BE的距离. 
【答案】
(1)解:由旋转的性质可知:∠BAE=∠DAG,由正方形的性质可知:AB=AD,AE=AG.
∵在△ABE和△ADG中, 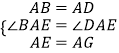 ,
,
∴△ABE≌△ADG.
∴BE=DG.
(2)解:连接GE、BG,延长AD交GE与H.
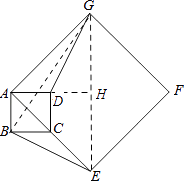
当α=45°时,则∠BAD=45°.
∵∠BAD=∠EAG=90°.
∴∠EAH=∠GAH=45°.
又∵AE=AG,
∴AH⊥GE.
又∵AH⊥AB,∠EAH=45°,
∴△AHE为等腰直角三角形.
∴EH=AH= ![]() AE=4.
AE=4.
∴EG=2EH=8.
∴S△BEG= ![]() EGAH=
EGAH= ![]() ×8×4=16.
×8×4=16.
设点G到BE的距离为h.
S△BEG= ![]() EBh=16,即
EBh=16,即 ![]() ×4
×4 ![]() h=16,解得h=4
h=16,解得h=4 ![]() .
.
∴点G到BE的距离为4 ![]()
【解析】(1)由旋转的性质得到∠BAE=∠DAG,由正方形的性质得到AB=AD,AE=AG,然后依据SAS可证明△ABE≌△ADG,然后依据全等三角形的性质进行证明即可;(2)连接GE、BG,延长AD交GE与H.当α=45°时,可证明△AHE为等腰直角三角形,然后可求得AH和HE的长,然后依据等腰三角形三线合一的性质可得到EG=2HE,最后在△BEG中,利用面积法可求得点G到BE的距离.
【考点精析】关于本题考查的正方形的性质和旋转的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.

【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完整: 
(1)函数y=|x﹣1|的自变量x的取值范围是;
(2)列表,找出y与x的几组对应值.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | b | 1 | 0 | 1 | 2 | … |
其中,b=;
(3)在平面直角坐标系xOy中,描出以上表中对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .