题目内容
【题目】如图,抛物线y= ![]() x(x﹣k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9
x(x﹣k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9
(1)求抛物线的解析式;
(2)点P为第一象限的抛物线上一点,连接PB、PC,设P点的横坐标为m,△PBC的面积为S,求S与m的函数关系式;
(3)在(2)的条件下,连接OP、AP,若∠APO=45°,求点P的坐标.
【答案】
(1)
解:如图1中,作BH⊥x轴于H.
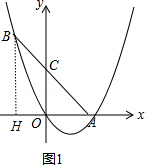
由题意OC=OA=K,∠AOC=90°,
∴∠OAC=∠OCA=45°,
∵∠BHA=90°,
∴∠HBA=∠HAB=45°,
∴BH=AH=9,
∴OH=9﹣k,
∴B(k﹣9,9),
把B(k﹣9,9)代入y= ![]() x(x﹣k),
x(x﹣k),
得到9= ![]() (k﹣9)×(﹣9),
(k﹣9)×(﹣9),
∴k=5,
∴抛物线的解析式为y= ![]() x(x﹣5).
x(x﹣5).
(2)
解:如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m, ![]() m(m﹣5)].
m(m﹣5)].
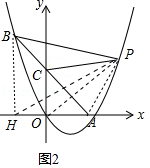
∵P(﹣4,9),A(5,0),C(0,5),
∴S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)
= ![]() ×9×(m+4)+
×9×(m+4)+ ![]() ×9×
×9× ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ×9×9﹣[
×9×9﹣[ ![]() ×5×m+
×5×m+ ![]() ×5×
×5× ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ×5×5]
×5×5]
= ![]() m2﹣m﹣10(m>5).
m2﹣m﹣10(m>5).
(3)
解:如图3中设AC交OP于D,AC的中点为K,连接PK.
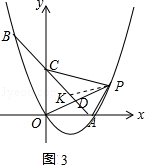
∵∠DPA=∠DCO=45°,∠PDA=CDO,
∴△PDA∽△CDO,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠CDP=∠ODP,
,∵∠CDP=∠ODP,
∴△CDP∽△ODA,
∴∠CPD=∠OAD=45°,
∴∠CPA=90°,
∵CK=KA,
∴PK= ![]() AC=
AC= ![]() ,
,
设P[m, ![]() m(m﹣5)],
m(m﹣5)],
∵K( ![]() ,
, ![]() ),
),
∴(m﹣ ![]() )2+[
)2+[ ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ]2=(
]2=( ![]() )2,
)2,
整理得m(m﹣5)(m2﹣5m﹣4)=0,
∴m=0或5或 ![]() 或
或 ![]() ,
,
∵m>5,
∴m= ![]() ,
,
∴P( ![]() ,1).
,1).
【解析】(1)如图1中,作BH⊥x轴于H.由题意OC=OA=K,∠AOC=90°,推出∠OAC=∠OCA=45°,由∠BHA=90°,推出∠HBA=∠HAB=45°,推出BH=AH=9,推出OH=9﹣k,推出B(k﹣9,9),把B(k﹣9,9)代入y= ![]() x(x﹣k),解方程即可.(2)如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m,
x(x﹣k),解方程即可.(2)如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m, ![]() m(m﹣5)].根据S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)计算即可.(3)如图3中设AC交OP于D,AC的中点为K,连接PK.只要证明∠CPA=90°,根据PK=
m(m﹣5)].根据S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)计算即可.(3)如图3中设AC交OP于D,AC的中点为K,连接PK.只要证明∠CPA=90°,根据PK= ![]() ,利用两点间距离公式,列出方程,解方程即可解决问题.
,利用两点间距离公式,列出方程,解方程即可解决问题.
【考点精析】本题主要考查了等腰直角三角形和函数关系式的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;用来表示函数关系的数学式子叫做函数解析式或函数关系式才能正确解答此题.

 小学教材全测系列答案
小学教材全测系列答案【题目】已知函数y=2+ ![]() .
.
(1)写出自变量x的取值范围:;
(2)请通过列表,描点,连线画出这个函数的图象: ①列表:
x | … | ﹣8 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ | | 1 | 2 | 3 | 4 | 8 | … |
y | … | | 1 | | 0 | ﹣2 | ﹣6 | 10 | 6 | 4 | | 3 | | … |
②描点(在下面给出的直角坐标系中补全表中对应的各点);
③连线(将图中描出的各点用平滑的曲线连接起来,得到函数的图象).
(3)观察函数的图象,回答下列问题: ①图象与x轴有个交点,所以对应的方程2+ ![]() =0实数根是;
=0实数根是;
②函数图象的对称性是 .
A、既是轴对称图形,又是中心对称图形
B、只是轴对称图形,不是中心对称图形
C、不是轴对称图形,而是中心对称图形
D、既不是轴对称图形也不是中心对称图形
(4)写出函数y=2+ ![]() 与y=
与y= ![]() 的图象之间有什么关系?(从形状和位置方面说明)
的图象之间有什么关系?(从形状和位置方面说明)







