题目内容
【题目】在平面直角坐标系xOy中,抛物线y=x2+mx+n﹣1的对称轴为x=2. 
(1)m的值为;
(2)若抛物线与y轴正半轴交于点A,其对称轴与x轴交于点B,当△OAB是等腰直角三角形时,求n的值;
(3)点C的坐标为(3,0),若该抛物线与线段OC有且只有一个交点,求n的取值范围.
【答案】
(1)-4
(2)解:把m=﹣4代入抛物线y=x2+mx+n﹣1得:
y=x2﹣4x+n﹣1,
当x=0时,y=n﹣1,
∴A(0,n﹣1),B(2,0),
∵△OAB是等腰直角三角形,
∴OA=OB,
即:n﹣1=2,n=3
(3)解:①如图1,当抛物线顶点在x轴上时,
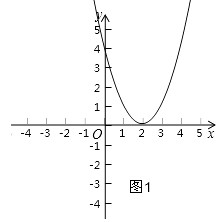
△=0,(﹣4)2﹣4×1×(n﹣1)=0
n=5,
②如图2,当抛物线过点C(3,0)时,

把(3,0)代入得:32﹣4×3+n﹣1=0,
n=4,
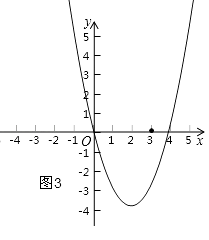
③如图3,当抛物线过原点时,n﹣1=0,n=1,
结合图象可得,1≤n<4或n=5.
【解析】解:(1)对称轴:x=﹣ ![]() =2,m=﹣4;
=2,m=﹣4;
【考点精析】本题主要考查了等腰直角三角形和抛物线与坐标轴的交点的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





