题目内容
【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完整: 
(1)函数y=|x﹣1|的自变量x的取值范围是;
(2)列表,找出y与x的几组对应值.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | b | 1 | 0 | 1 | 2 | … |
其中,b=;
(3)在平面直角坐标系xOy中,描出以上表中对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .
【答案】
(1)任意实数
(2)2
(3)解:如图所示
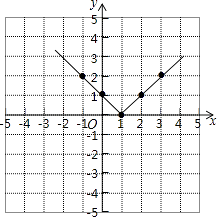
(4)函数的最小值为0(答案不唯一)
【解析】解:(1)∵x无论为何值,函数均有意义, ∴x为任意实数.
所以答案是:任意实数;
⑵∵当x=﹣1时,y=|﹣1﹣1|=2,
∴b=2.
所以答案是:2;
⑷由函数图象可知,函数的最小值为0.
所以答案是:函数的最小值为0(答案不唯一).
【考点精析】认真审题,首先需要了解一次函数的性质(一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小),还要掌握一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远)的相关知识才是答题的关键.

【题目】已知函数y=2+ ![]() .
.
(1)写出自变量x的取值范围:;
(2)请通过列表,描点,连线画出这个函数的图象: ①列表:
x | … | ﹣8 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ | | 1 | 2 | 3 | 4 | 8 | … |
y | … | | 1 | | 0 | ﹣2 | ﹣6 | 10 | 6 | 4 | | 3 | | … |
②描点(在下面给出的直角坐标系中补全表中对应的各点);
③连线(将图中描出的各点用平滑的曲线连接起来,得到函数的图象).
(3)观察函数的图象,回答下列问题: ①图象与x轴有个交点,所以对应的方程2+ ![]() =0实数根是;
=0实数根是;
②函数图象的对称性是 .
A、既是轴对称图形,又是中心对称图形
B、只是轴对称图形,不是中心对称图形
C、不是轴对称图形,而是中心对称图形
D、既不是轴对称图形也不是中心对称图形
(4)写出函数y=2+ ![]() 与y=
与y= ![]() 的图象之间有什么关系?(从形状和位置方面说明)
的图象之间有什么关系?(从形状和位置方面说明)