题目内容
【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3cm,AD=2cm,EF= ![]() EH,求EH的长.
EH,求EH的长. 
【答案】解:∵四边形EFGH是矩形, ∴EH∥BC,
∴△AEH∽△ABC,
∵AD⊥BC,AM⊥EH,
∴ ![]() =
= ![]() ,即
,即 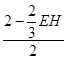 =
= ![]() ,
,
解得,EH= ![]() cm.
cm.
【解析】根据矩形的性质得到EH∥BC,得到△AEH∽△ABC,根据相似三角形的性质列出比例式,计算即可.
【考点精析】根据题目的已知条件,利用矩形的性质和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目






