题目内容
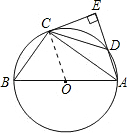
如图所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O上，过点C的切线交AD的延长线于点E，且
AE⊥CE，连接CD．
（1）求证：DC=BC；
（2）若AB=5，AC=4，求tan∠DCE的值．
AE⊥CE，连接CD．（1）求证：DC=BC；
（2）若AB=5，AC=4，求tan∠DCE的值．
（1）证明：连接OC． （1分）
∵OA=OC，
∴∠OAC=∠OCA．
∵CE是⊙O的切线，
∴∠OCE=90°． （2分）
∵AE⊥CE，
∴∠AEC=∠OCE=90°．
∴OC∥AE． （3分）
∴∠OCA=∠CAD．
∴∠CAD=∠BAC． （4分）
∴
=
．
∴DC=BC． （5分）
（2）∵AB是⊙O的直径，
∴∠ACB=90°．
∴BC=
=
=3． （6分）
∵∠CAE=∠BAC，∠AEC=∠ACB=90°，
∴△ACE∽△ABC． （7分）
∴
=
．
∴
=
EC=
． （8分）
∵DC=BC=3，
∴ED=
=
=
．（9分）
∴tan∠DCE=
=
=
．（10分）
∵OA=OC，
∴∠OAC=∠OCA．
∵CE是⊙O的切线，
∴∠OCE=90°． （2分）
∵AE⊥CE，
∴∠AEC=∠OCE=90°．
∴OC∥AE． （3分）
∴∠OCA=∠CAD．
∴∠CAD=∠BAC． （4分）
∴
 |
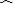| DC |
|
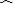| BC |
∴DC=BC． （5分）
（2）∵AB是⊙O的直径，
∴∠ACB=90°．
∴BC=
| AB2-AC2 |
| 52-42 |
∵∠CAE=∠BAC，∠AEC=∠ACB=90°，
∴△ACE∽△ABC． （7分）
∴
| EC |
| BC |
| AC |
| AB |
∴
| EC |
| 3 |
| 4 |
| 5 |
| 12 |
| 5 |
∵DC=BC=3，
∴ED=
| DC2-CE2 |
32-(
|
| 9 |
| 5 |
∴tan∠DCE=
| ED |
| EC |
| ||
|
| 3 |
| 4 |
练习册系列答案
名校课堂系列答案
相关题目
山脚点A测得山腰上一点D的仰角为300，并测得AD的长度为180米；另一部分同学在山顶点B测得山脚点A的俯角为450，山腰点D的俯角为600。请你帮助他们计算出小山的高度BC（计算过程和结果都不取近似值）。
的速度向B移动，到达B后停止；t（秒）为E点移动的时间．
