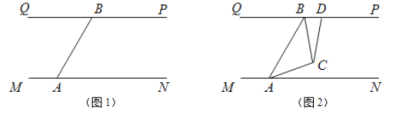Question

【题目】如图，某大楼的顶部竖有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底仰角为60°，沿坡度为1： 的坡面AB向上行走到B处，测得广告牌顶部C的仰角为45°，又知AB=10m，AE=15m，求广告牌CD的高度（精确到0.1m，测角仪的高度忽略不计）

Answer 1

【答案】解：在Rt△ABH中，

∵tan∠BAH= = = ，

∴∠BAH=30°，

∴BH=AB，sin∠BAH=10，sin30°=10× =5，

在Rt△ABH中，AH=AB．cos∠BAH=10，cos30°=5 ，

在Rt△ADE中，tan∠DAE= ，

即tan60°= ，

∴DE=15 ，

如图，过点B作BF⊥CE，垂足为F，

∴BF=AH+AE=5 +15，

DF=DE﹣EF=DE﹣BH=15 ﹣5，

在Rt△BCF中，∠C=90°﹣∠CBF=90°﹣45°=45°，

∴∠C=∠CBF=45°，

∴CF=BF=5 +15，

∴CD=CF﹣DF=5 +15﹣（15 ﹣5）=20﹣10 ≈20﹣10×1.732≈2.7（米），

答：广告牌CD的高度约为2.7米．

【解析】过点B作BF⊥CE，垂足为F，通过解直角三角形求出BH、AH，在△ADE解直角三角形求出DE的长，进而可求出EH即BF的长，在Rt△CBF中，∠CBF=45°，则CF=BF，由此可求出CF的长，最后，根据CD=CF+FE-DE求解即可.