Question

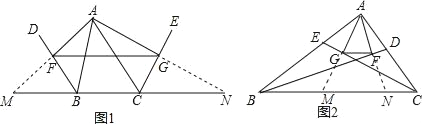
【题目】如图1，O为直线AB上一点，过点O作射线OC，，将一直角三角板的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．

将图1中的三角板绕点O以每秒的速度沿逆时针方向旋转一周如图2，经过t秒后，ON落在OC边上，则______秒直接写结果．

如图2，三角板继续绕点O以每秒的速度沿逆时针方向旋转到起点OA上同时射线OC也绕O点以每秒的速度沿逆时针方向旋转一周，

当OC转动9秒时，求的度数．

运动多少秒时，？请说明理由．

Answer 1

【答案】（1）6；（2）①②11秒或25秒，理由见解析.

【解析】

(1)因为∠AOC=30°，所以ON落在OC边上时，三角板旋转了30°，即可求出旋转时间；

(2)在整个旋转过程中，可以看做这样一个追及问题更容易理解，即：ON绕点O以每秒5°的速度沿逆时针方向旋转，同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转；

①9秒时，∠NOC=45°，而OC旋转了90°，所以∠MOC的度数就是45°；

②∠MOC=35°时，应分OC与OM重合前35°与重合后35°两种情况考虑，分别进行求解即可.

，

而三角板每秒旋转，

当ON落在OC边上时，有，

得，

故答案为6；

当OC转动9秒时，，

而，

又，

即：，

答：当OC转动9秒时，的度数为；

设OC运动起始位置为射线如图，运动t秒时，，

则，，

当时，有或，

得或，

因为三角板与射线OC都只旋转一周，所以不考虑再次追及的情况，

故当运动11秒或25秒时，．